Today's Challenge

Let's dive into the problem at hand:

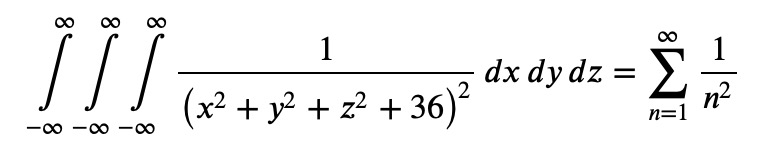
Solving with SymPy

The straightforward part of this exercise is the infinite sum, which is well-documented (for instance, check this article) and can be handled directly by SymPy:

Why Coordinate Transforms Matter

Utilizing Python's SymPy along with Parseval’s Theorem allows for the evaluation of infinite series effectively.

The more challenging aspect is the triple integral. Let’s attempt to tackle it directly:

As anticipated, SymPy takes some time and ultimately fails. However, we can aid the process by applying a coordinate transformation. The denominator in our integrand is reminiscent of the squared distance in spherical coordinates, prompting us to convert from Cartesian to spherical coordinates. The transformation is given by:

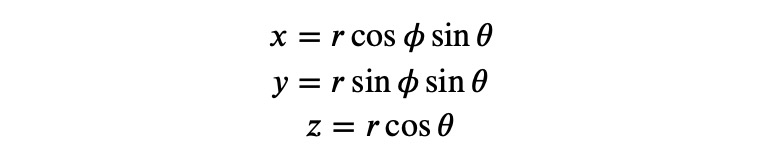
To execute the transformation within the integral, we require the Jacobian—the determinant of the functional matrix. Let's implement a small function to calculate this:

In our scenario, the Jacobian simplifies to:

In Cartesian coordinates, we integrate over the entire space. In spherical coordinates, this translates to integrating ( r ) from 0 to infinity, ( theta ) from 0 to ( 2pi ), and ( phi ) from 0 to ( pi ). We can now construct the transformed integrand:

Next, we proceed to compute the integral:

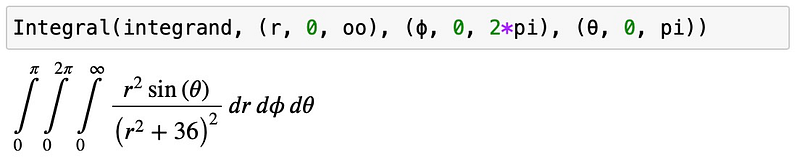
This concludes our exploration for today. I look forward to seeing you in the next session!

A detailed guide on computing integrals through coordinate transformations.

Tutorial on using SymPy to evaluate integrals effectively.