Understanding Mathematical Induction: The Domino Principle
Written on
Introduction to Mathematical Induction
In this discussion, we will explore a vital proof technique used to establish properties of natural numbers (or any mathematical structures with minimal elements). Many of you may already be familiar with mathematical induction, which asserts that to prove a property for every positive natural number ( N ), one must:
- Demonstrate that the property holds for ( N = 1 ).
- Show that if the property is true for a natural number ( N ), it must also be true for ( N + 1 ).
These steps are fundamental: the first is known as the base case, while the second is termed the inductive step. We will now refine these concepts and examine some examples.
To illustrate, let’s denote a property that depends on a natural number ( N ) as ( P(N) ). For instance:
- ( P(N) ): "The number ( N ) is divisible by 2."
- ( P(N) ): "The expression ( (N + 1)^2 ) is non-negative."
The first statement is only valid for even numbers, while the second holds true for all natural numbers. To establish that a statement is true for all natural numbers, we can use the outlined strategy.
Understanding the Induction Process
The first requirement is to identify a starting point, which can be any natural number (including 0). The validity of the statement will then extend to all natural numbers greater than or equal to this base case.
For example, if we prove that ( P(N) ) holds for a natural number ( N = k ), we can then demonstrate that:
- ( P(k + 1) ) is true.
- Continuing this process, we can show that ( P(k + 2), P(k + 3), ) and so on, are also true.
This sequence generates a proof that ( P(N) ) is valid for every number greater than or equal to our base case. The essence of mathematical induction is that if both the base case and the inductive step are verified, the process will always be reliable. The domino effect serves as a fitting analogy: the inductive step ensures that "if one domino falls, the next will follow," while the base case guarantees that "the first domino is pushed."

Visualizing the Induction Process
Mathematical induction is not just applicable to natural numbers; it can also be used for finite sets of natural numbers. For example, one can prove that a property holds for every natural number from 1 to ( M ) (where ( M geq 1 )) using the same approach.
A variant called strong induction can also be helpful. In this case, the inductive step is modified to state:
(2') Show that if the property holds for every positive natural number less than or equal to ( N ), then it must also hold for ( N + 1 ).
A notable case where standard induction does not apply is with real numbers, as there is no clear base case or a defined "next" real number for the inductive step. However, advanced forms of induction, such as transfinite induction, are available for uncountable sets, though these are beyond the scope of this article.
Examples of Mathematical Induction
To clarify the concepts discussed, we will examine two examples.
Example 1: Proving a Statement for Natural Numbers
Show that the following statement is true for every natural number ( N > 0 ):
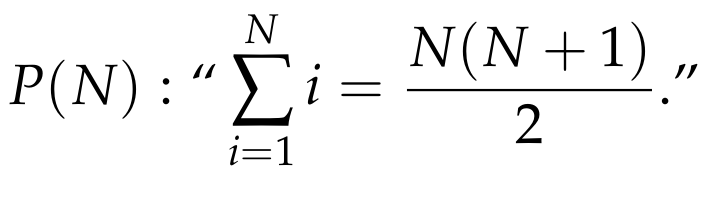
Using standard mathematical induction, we first establish our base case:
- For ( N = 1 ), both sides of the statement equal 1, confirming the base case.
Next, for the inductive step, we assume the statement is true for ( N = k ) (our inductive hypothesis) and demonstrate that it holds for ( N = k + 1 ).
The first video titled "Proof by Mathematical Induction: Mathematical Dominoes" provides an insightful visual representation of this proof technique, enhancing our understanding of the induction process.
Example 2: Properties of Rooted Binary Trees
Now, let’s consider a statement concerning rooted binary trees. A rooted binary tree consists of a root node and can have up to two children. Each child is itself a rooted binary tree, ensuring no cycles exist.
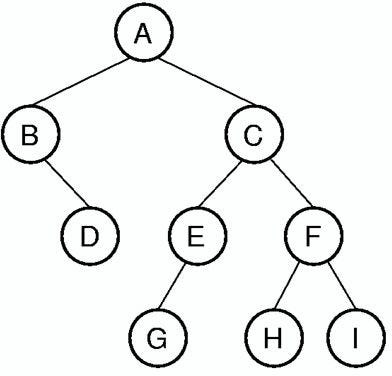
We are interested in proving that the following statement holds for every ( N geq 0 ):

First, we verify the base case: a binary tree with height 0 consists of one vertex, making its size 1, which satisfies ( 2^0 - 1 ).
For the inductive step, assume the statement is valid for all binary trees of height at most ( N ). We will show it holds for trees of height ( N + 1 ). A tree of height ( N + 1 ) has a root node and at least one child, leading us into two cases based on the number of children.
The second video titled "Mathematical induction and the domino effect - A visual explanation" provides additional insights into the application of induction in various contexts, reinforcing the concepts we have explored.
Through these examples, we can see how mathematical induction serves as a powerful tool in proving statements related to natural numbers and structured mathematical entities.