Understanding the Distinction Between Maximum and Minimum Values
Written on
Chapter 1: Weekly Challenge Recap
This week's challenge appears to be a bit more straightforward compared to previous ones. Regardless, let's give a round of applause to this week's top performers! 1st Place: Alfredo Esposito 7 Points 🎉 2nd Place: Neil Faver 5 Points 🎉 3rd Place: Wotsit 3 Points 🎉 Other Participants: Aaron Tovish, Jonathan Lynn Harvey 1 Point each 🎉
Here’s the solution! We can start by rearranging the two equations to consolidate all terms involving 'a' and 'b' on one side.
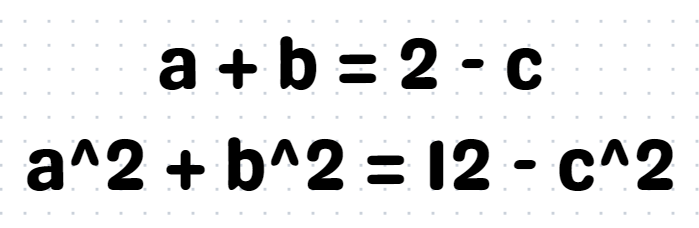
The key to solving this problem is to embrace the idea of treating 'x' as a variable.
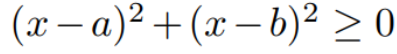
This inequality holds true since we are summing two squared terms, and each squared term must be zero or greater. Upon expanding the terms, we derive the following quadratic inequality.
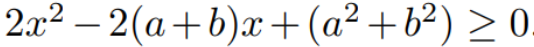
Note that the expressions (a + b) and (a² + b²) can be expressed in terms of 'c'.
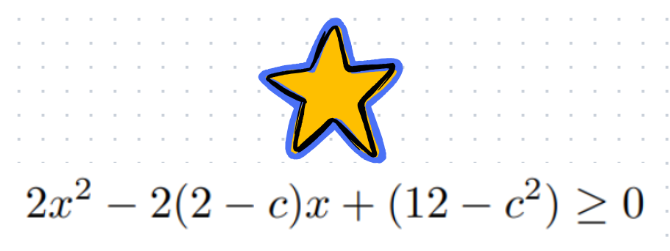
Now we have a quadratic inequality that is greater than or equal to zero, with coefficients expressed in terms of 'c'. Remember from high school algebra that a quadratic equation has two distinct real roots if the discriminant is greater than zero, one repeated root if it equals zero, and no real roots if it is less than zero. Our quadratic equation must be greater than or equal to zero, indicating that it either has no real roots or it touches the x-axis at one point. Hence, we can conclude that its discriminant must be less than or equal to zero.

Hopefully, you recall that b² - 4ac is the essential formula. We can simplify this quadratic inequality in terms of 'c'.
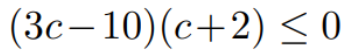
Thus, the range of 'c' is determined.
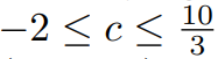
Let’s now calculate the minimum of 'c' by letting c = -2.
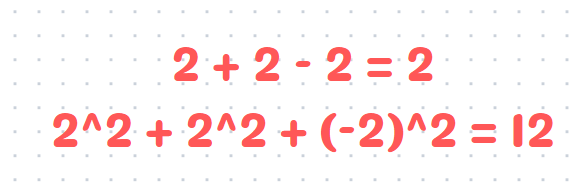
So, the minimum of 'c' is -2. Now, let's evaluate the maximum of 'c' by letting c = 10/3.
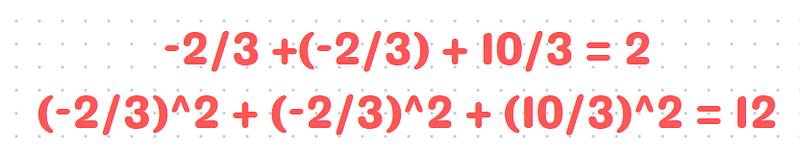
Consequently, the maximum of 'c' is 10/3. Finally, we can find the difference.

Therefore, the answer is D. How did you perform in the sixth Math Games? Looking forward to seeing you next week, challengers!

Chapter 2: Video Resources
In this video, viewers will learn how to find the difference between the maximum and minimum values for various groups.
This video offers insights into the differences between local and absolute minima and maxima, specifically tailored for VCE Maths Methods.