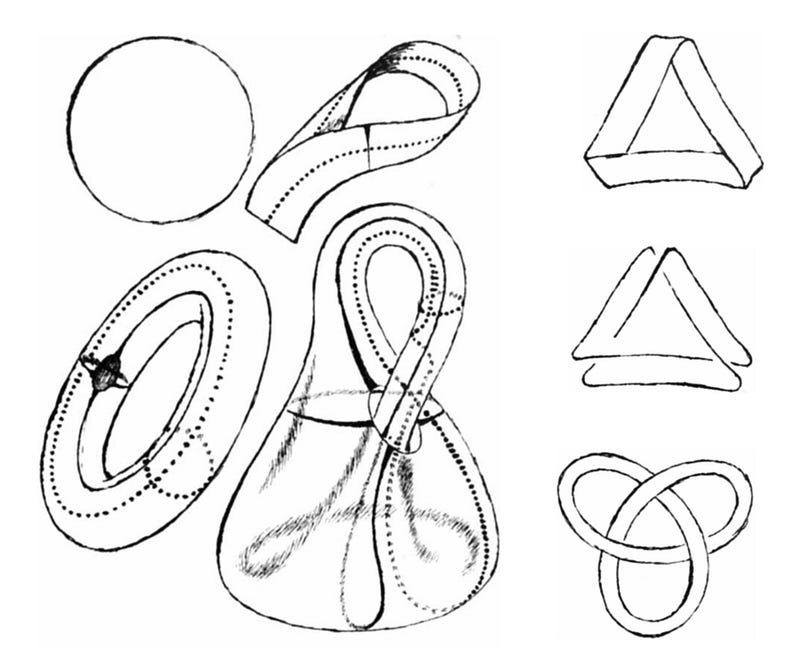
Chapter 2: A Mathematical Wonder

The Klein Bottle can only exist in four-dimensional space without self-intersection. To help us visualize this perplexing object, we often rely on a three-dimensional model that necessitates self-intersection.

Mathematically, the Klein Bottle can be described through specific equations in four-dimensional Euclidean space:

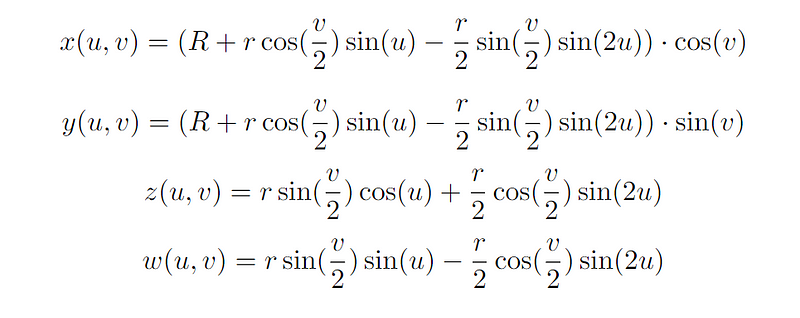
These equations define the coordinates (x, y, z, w) of points on the Klein Bottle surface based on parameters u and v. The Klein Bottle Hat serves as a three-dimensional approximation of the Klein Bottle, emphasizing the connection between these mathematical equations and the hat itself.

The parameters u and v range from 0 to 2π, enabling us to map points on the Klein Bottle's surface. R represents the radius of the larger circle forming the "body," while r denotes the radius of the smaller circles that create the "neck" and "base" of the Bottle.

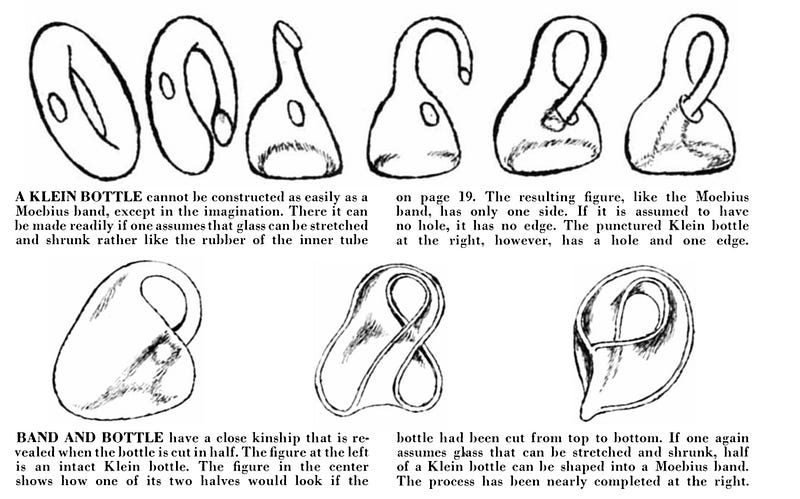
The equations x(u, v) and y(u, v) define the x and y coordinates of points on the Klein Bottle, controlling the overall shape and positioning of the large and small circles. The z(u, v) equation determines the height of the surface, shaping the "neck" of the Klein Bottle, which loops back to connect with its "body." The w(u, v) equation represents the fourth coordinate in four-dimensional space. While this coordinate lacks a direct counterpart in the three-dimensional Klein Bottle Hat, it is vital for representing the non-orientable characteristic of the true Klein Bottle.

When crafting the Klein Bottle Hat, we approximate the Klein Bottle in three-dimensional space, inevitably sacrificing some four-dimensional properties. Consequently, the hat's surface intersects itself, a feature absent in the authentic Klein Bottle.

Chapter 3: Topological Features of the Klein Bottle Hat

Although a true Klein Bottle cannot exist in three-dimensional space without self-intersecting, the Klein Bottle Hat provides an approximate representation that captures the essence of its mathematical origin.

Non-Orientability:

Both the Klein Bottle and its hat counterpart are non-orientable surfaces, lacking well-defined “inside” and “outside.” When tracing a path along the hat’s surface, one eventually returns to the starting point without crossing an edge. This quality can be illustrated mathematically by the fact that the hat has a single continuous side.

Self-Intersection:

To reflect the Klein Bottle's four-dimensional characteristics in our three-dimensional world, the surface of the Klein Bottle Hat must self-intersect. This intersection, typically found at the crown of the hat, represents a necessary trade-off that allows the hat to embody the spirit of the Klein Bottle while remaining a functional accessory.

Homotopy:

The Klein Bottle Hat demonstrates homotopy equivalence with the Klein Bottle, implying that a continuous deformation (homotopy) exists between the two surfaces. This connection underscores the relationship between the hat and its mathematical inspiration, asserting that the hat is a valid approximation of the Klein Bottle in a wearable form.

As you contemplate the enigma of the Klein Bottle Hat, consider this intriguing question:

Given that the Klein Bottle is a non-orientable surface that can only exist without self-intersection in four-dimensional space, what other higher-dimensional objects or topological transformations could potentially be adapted or approximated into our three-dimensional world while preserving their most fascinating and counterintuitive properties?

Let the Klein Bottle Hat motivate you to explore the captivating world of topology and challenge your perceptions of space, dimensions, and the underlying mathematical structures that shape our reality.

And that’s our exploration.

How remarkable is that?

What are your thoughts on this topic? Feel free to share in the comments below; I’m excited to hear from you!

Math Puzzles

The best math puzzles on Medium, including Algebra, Geometry, Calculus, Number Theory, and more.

This video reviews and tests concepts from Chapter 5 of GoMath!, illustrating the application of the Klein Bottle in mathematical puzzles.

In this video, ECON 2301 Mindtap discusses Chapter 5, providing examples and insights related to the Klein Bottle's mathematical properties.

Thank you for reading! If you found this article insightful, please let me know by clapping or sharing it with others.