Chapter 1: Introduction to the Geometry Puzzle

In this article, I present another captivating geometry challenge that has gained popularity online. I stumbled upon this puzzle recently and found it quite intriguing. As is typical with viral math puzzles, pinpointing its original source proved difficult, as I encountered it from various platforms before deciding to delve deeper.

This particular puzzle involves a right-angled isosceles triangle, where both equal sides measure 4 units. Inside this triangle lies an inscribed circle that touches all three sides. Your task is to determine the area of this inscribed circle. Do you think you can crack it?

Spoiler Alert:

In the following sections, I will reveal the solution to this puzzle. If you prefer to attempt solving it independently first, now is the perfect time to do so. Once you’ve made your effort, feel free to return and see how our methods compare.

Section 1.1: Preparing to Solve the Geometry Puzzle

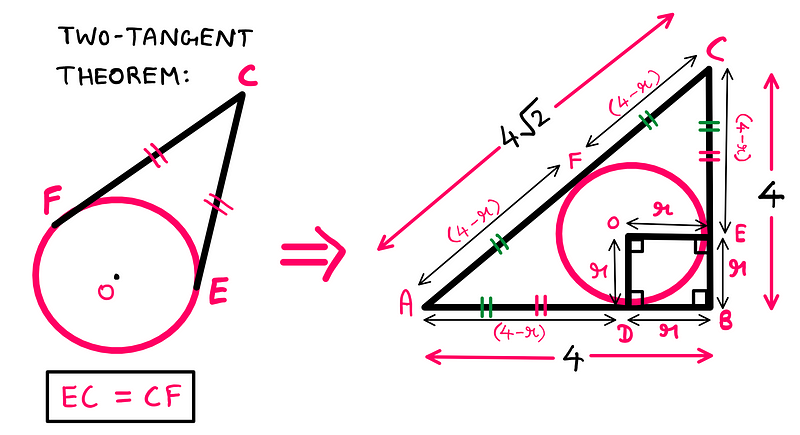
To start, I recommend labeling the key points and vertices as illustrated below. This will simplify our calculations as we move forward. The center of the circle has been designated as ‘o’.

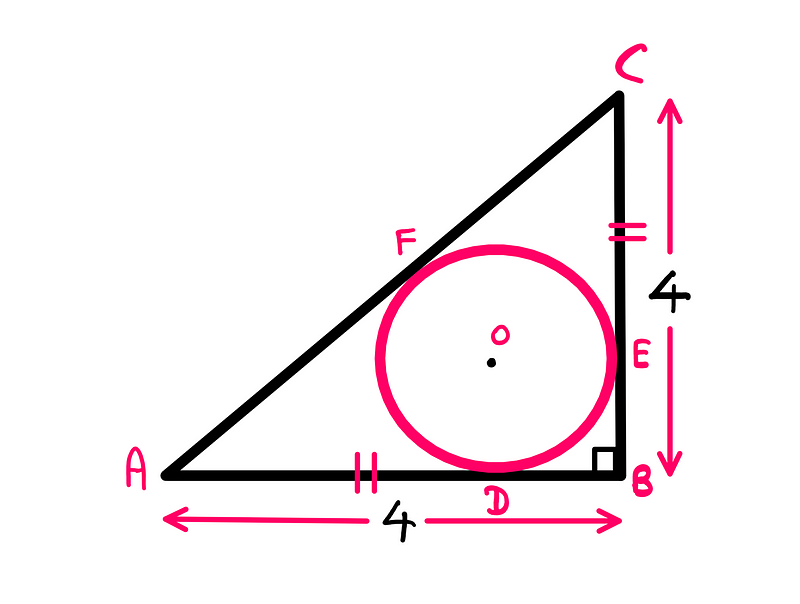
So far, we have established the following:

AB = BC = 4 units

Utilizing the Pythagorean theorem, we can calculate the unknown hypotenuse AC as follows:

AC² = AB² + BC²

? AC² = 4² + 4² = 16 + 16 = 32

? AC = √32 = √(2*16)

? AC = 4√2 units (considering positive lengths only)

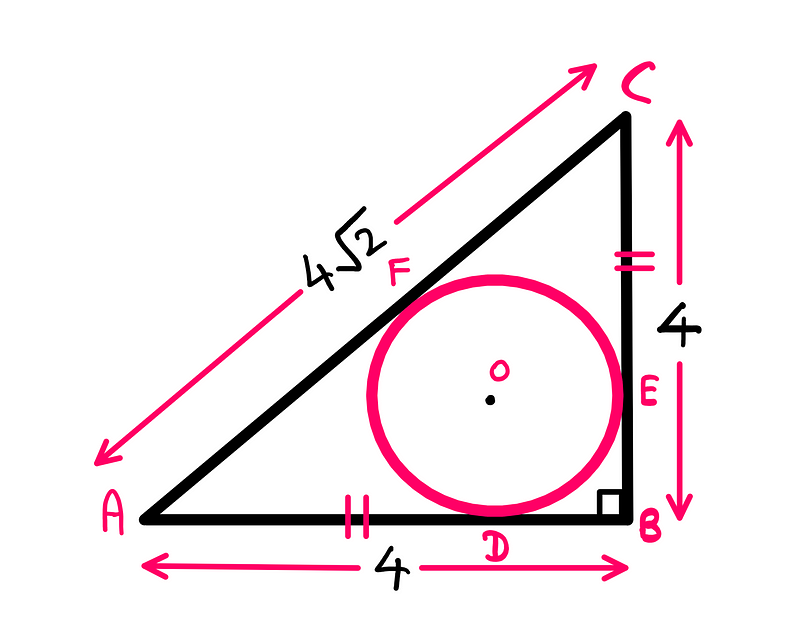
Now that we know the length of AC is 4√2 units, we can begin to establish a mathematical relationship between the circle and the triangle's sides.

Section 1.2: Utilizing the Tangent-to-Circle Theorem

Let’s examine the two equal sides of the triangle: AB and BC. Since these sides form a right angle, we can leverage this information effectively.

Let’s draw straight lines from the center of the circle ‘o’ to the points where the circle touches AB (D) and BC (E).

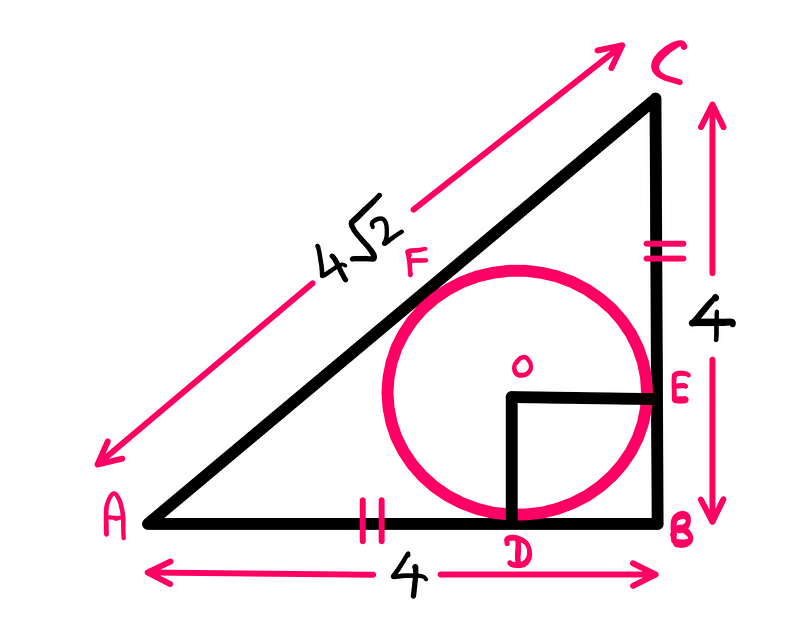
The tangent-to-circle theorem states:

A tangent to a circle is always perpendicular to the radius at the point of contact.

If you have been attentive, you may have noticed that OD and OE are of equal length (since both are radii). Using this insight, we can visualize the square ODBE, where we will assign the variable ‘r’ to represent the unknown radius of the circle.

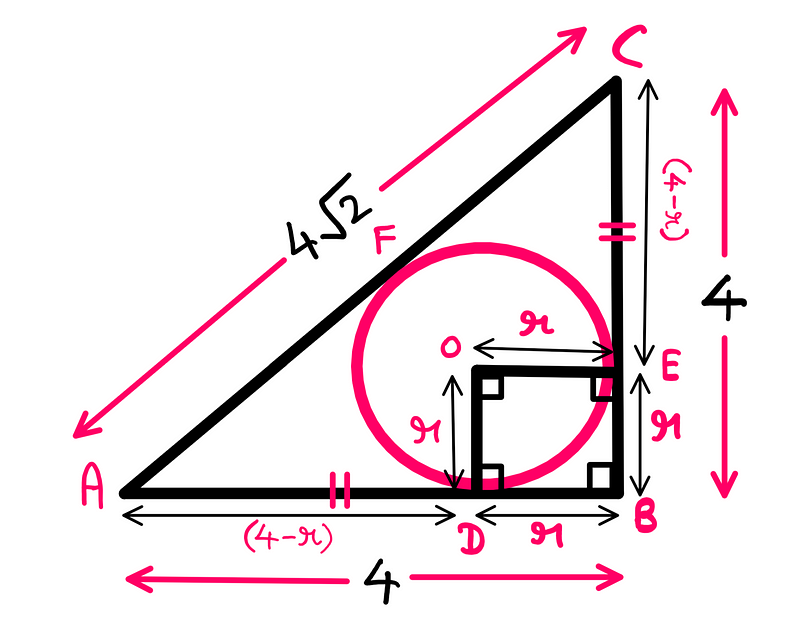
Since ODBE forms a square, the lengths of DB and DE are both equal to ‘r’. Thus, we can deduce that AD = (4 — r) units, which is also equal to EC. We’re getting closer to solving this puzzle!

Section 1.3: Applying the Two-Tangent Theorem

The two-tangent theorem states:

When two tangents are drawn from the same external point to a circle, the segments from that point to the circle are equal in length.

In our setup, this means that AD must equal FA, and EC must equal CF. Therefore, we can conclude:

AD = FA = EC = CF = (4 — r) units.

We are nearly there. Let's complete the solution!

Chapter 2: Finalizing the Geometry Puzzle Solution

We now have all the necessary components to solve this geometry puzzle. Let’s focus on the hypotenuse: CA. We know that CA = 4√2 units. Additionally, CA can be expressed as CF + FA, leading us to:

CA = CF + FA = 4√2 (units)

? CA = (4 — r) + (4 — r) = 4√2

? 8 – 2r = 4√2

Subtracting 8 from both sides gives:

? -2r = 4√2 – 8

Multiplying both sides by (-1) yields:

? 2r = 8 – (4√2)

Dividing by 2 results in:

r = [4 – (2√2)] units

Now that we have determined the radius of the circle, we can substitute this value into the familiar area formula for circles to calculate its area:

Area of the circle = πr² = π[4 – (2√2)]² = approximately 4.3121 units² (rounded to four decimal places).

There you have it! The area of the inscribed circle is approximately 4.3121 units².

For further exploration, you might find interest in: "Can You Actually Solve This Viral Geometry Puzzle (I)" and "How to Effectively Tackle Tricky Algebra Problems."

If you appreciate my work as an author, consider supporting me on Patreon.