Chapter 1: The Origins of Computational Complexity

In the 1960s and 70s, it became apparent that developing programs that operated without errors was not sufficient. The efficiency of these programs, particularly their runtime, emerged as a critical factor; after all, a program that never completes is of little value. Consequently, programmers sought innovative methods to enhance the speed of their programs, replacing slower algorithms with more efficient ones.

Before diving deeper into this topic, let's clarify what we mean by fast and slow programs through an engaging example. The sequence of operations a program follows is termed an algorithm, which can vary in efficiency.

Consider the classic "guess a number" game. You choose a number from a range, say between 1 and n, and after each guess, the host indicates whether your guess is too high or too low. The key question arises:

“How many guesses does it take to guarantee finding the correct number?”

One approach is the brute force method, where you guess sequentially: 1, 2, 3, and so on, until you find the right one. This algorithm operates with a runtime of n in the worst-case scenario and an average runtime of n/2. Thus, we denote its complexity as O(n) (read as "big O of n"), indicating that the runtime does not exceed cn for some constant c when n is sufficiently large. This is often referred to as “linear time.” Notably, this notation helps simplify expressions; for example, an² + bn + c = O(n²).

Now, we can ponder:

“Is there a more efficient algorithm than the brute force method?”

Indeed, the optimal strategy utilizes the feedback from the “higher or lower” hints effectively. By selecting the midpoint (n/2 for even n or (n+1)/2 for odd n), you can halve the potential numbers each time the host provides guidance. This technique is known as binary search and is commonly used alongside sorting algorithms. In computer science, the method of breaking a problem into smaller, similar subproblems and addressing them is referred to as “divide and conquer.”

This algorithm achieves a runtime of O(log n), where the logarithm is to base 2, significantly outperforming the brute-force approach. For instance, if you play this game with numbers from 1 to 1000, you would require at most 10 guesses. It might be fun to challenge a teenager in your household to see if they can guess the number while you place a wager on chores!

When programming, it’s crucial to consider these runtime principles. For example, iterating through a list of n elements results in O(n) complexity, while a nested loop leads to O(n²), and a triple nested loop escalates to O(n³). O(n²) is not optimal, but it pales in comparison to poorly structured recursive functions that could result in exponential runtime. Even today’s computers would struggle, taking an eternity to compute something as simple as the 100th Fibonacci number if efficiency isn’t prioritized.

Chapter 2: The Classes P and NP

As computer scientists made strides in developing efficient algorithms for certain problems, they recognized the need for a framework to categorize problems based on their computational complexity. Some problems are provably tied to exponential runtime or worse. Such proofs save time by indicating that no faster algorithms exist.

Conversely, we find problems that can be resolved in polynomial time, like sorting a list of n elements. When we say the complexity is polynomial, we mean there exists an algorithm that can solve the problem in O(n^k) steps for some constant k, where n represents the number of input parameters. The set of problems solvable in polynomial time is designated as P. Typically, these problems are decision problems, which can be simplified to asking whether a list is sorted rather than sorting it outright.

The class NP (nondeterministic polynomial time) encompasses decision problems verifiable in polynomial time. For instance, while solving a Sudoku puzzle might be challenging, verifying if a specific candidate is a solution is straightforward.

The pivotal question arises: are P and NP equivalent? Is it true that if a problem can be quickly verified, it can also be solved quickly? This notion may seem paradoxical, as the processes of checking a solution and deriving one appear fundamentally different. As MIT professor Scott Aaronson eloquently puts it, if P equals NP, the implications for society would be profound, erasing the distinction between creative problem-solving and merely recognizing solutions.

Despite the significance of this question, a definitive proof remains elusive. The Clay Mathematics Institute even placed a $1 million prize in the year 2000 for anyone who can resolve it.

To illustrate, we know that P ⊆ NP, as any problem solvable in polynomial time is verifiable in polynomial time. To demonstrate that P ≠ NP, one would need to identify an NP problem that is not part of P, meaning there’s no rapid algorithm for solving it, despite the ease of verifying its solution.

If it turns out that P = NP, our technological advancements would lag significantly, as many critical algorithms (like those addressing the traveling salesman problem, protein folding, and circuit design) would have fast solutions that currently elude us.

Historically, some problems transitioned from NP to P as clever solutions were discovered, while others remain stubbornly challenging.

Chapter 3: NP-Completeness and Its Implications

Notably, some NP problems pose greater challenges than others. The toughest among them belong to a subclass known as NP-complete. These problems possess the remarkable feature that solving one NP-complete problem would facilitate solutions for all NP problems in polynomial time.

This transformation, or reduction, of any NP problem to a specific NP-complete problem must occur in polynomial time. The implication is clear: if it can be proven that just one NP-complete problem resides in P (is solvable in polynomial time), then P = NP.

To elucidate this reduction concept, let’s consider a game in which two players alternately select numbers from a list ranging from 1 to 9, without replacement. The first player to achieve a sum of 15 wins.

Can we cleverly convert this problem into a different known problem? By transforming the list [1, 2, 3, 4, 5, 6, 7, 8, 9] into a matrix structure where each row, column, and diagonal sums to 15, we create a magic square.

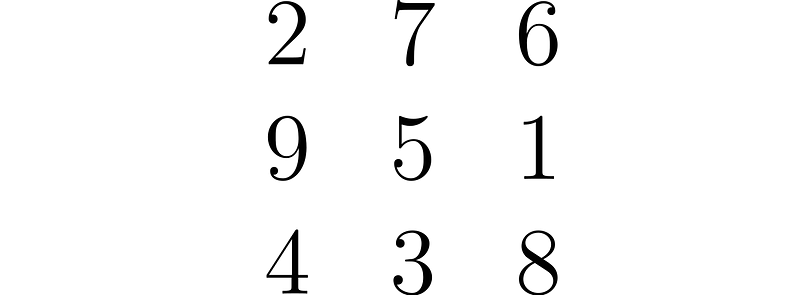
In this scenario, the objective shifts to being the first to pick three numbers in a row, column, or diagonal that total 15, resembling tic-tac-toe. Solving this tic-tac-toe scenario implies a solution to the original sum problem.

This reduction technique exemplifies the NP-completeness property, termed NP-hard. While NP-complete problems reside within NP, NP-hard problems may not. Consequently, NP-hard challenges can be even more complex than any NP problem.

The essential takeaway is this: each NP-complete problem is at least as challenging as any NP problem.

Chapter 4: The Complexity Landscape

The generalized Sudoku puzzle (potentially larger than the traditional 9 × 9 format) is recognized as NP-complete. If a method could be devised to solve Sudoku in polynomial time relative to the number of cells, it would confirm P = NP, since any NP problem could be translated into Sudoku in polynomial time.

However, achieving this seems unlikely. Generally, candidates for proving P ≠ NP are believed to exist among NP-complete problems.

The multitude of computational complexity classes presents a labyrinth of intersections, many of which remain under investigation.

The challenge lies in structuring the problems for effective mathematical scrutiny. An NP-complete problem is akin to seeking a needle in a haystack, where traditional methods yield little hope. The quest is to find a “magnet” that swiftly identifies solutions to these intricate problems.

If you enjoy articles like this one on Medium, consider subscribing for full access: simply click here.

Thank you for reading.

The first video titled "P vs. NP - The Biggest Unsolved Problem in Computer Science" provides an in-depth exploration of this critical question and its far-reaching implications in the field.

The second video titled "P vs. NP: The Biggest Puzzle in Computer Science" delves into the historical context and the ongoing quest for a solution to this pivotal challenge.