Understanding Information Gain: A Comprehensive Overview
Written on
Chapter 1: Introduction to Information Gain
Have you ever wondered what information gain really means? Let's explore this concept from three distinct perspectives!

Photo by Andrea Piacquadio from Pexels
Information gain serves as the backbone for decision trees, acting as a crucial factor in determining how attributes branch. Without information gain, decision trees would likely become excessively deep yet ineffective.
This leads us to the question: What exactly is information gain? Before diving into that, it's essential to grasp its prerequisite—entropy. In simple terms, entropy quantifies the randomness within a system. For further insights on entropy, check out this reference.
With a basic understanding of entropy in place, let's delve into the concept of information gain.
Section 1.1: The Mathematical Perspective
The mathematical definition of information gain can be expressed as follows:
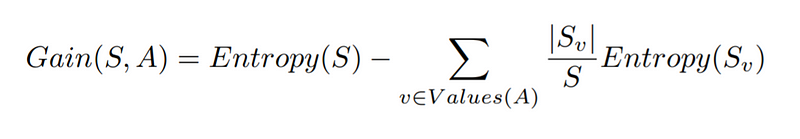
Source: Author
In this equation, S represents your dataset, A signifies an attribute of the data, and S? is the subset of data corresponding to the various values of A.
The first component of the formula refers to the entropy of the entire dataset, illustrating the overall randomness present. The second part sums the entropies when the different values of A are identified.
For instance, if attribute A can assume two values, we calculate the entropies for both and then combine them. S? denotes how many times a specific value of attribute A appears, while S indicates the total data points in the dataset.
Entropy(S?) is derived from the specific value of attribute A. For example, if attribute A takes on the value x, yielding 8 positive and 16 negative examples, we compute entropy based on these figures. Similarly, for value y, with 9 positive and 14 negative examples, the entropy is calculated accordingly.
The gain arises from the difference between these calculations. The greater the gain, the more entropy can be reduced by utilizing that attribute for branching in the decision tree.
Section 1.2: The Intuitive Approach
When we look at the formula for information gain, we observe that the entropy of the system is reduced by the summation of entropies when one of the attribute’s values is known.
This establishes an apples-to-apples comparison, illustrating that entropy is subtracted from entropy. But why is this beneficial? By revealing a single attribute’s value at a time, we can evaluate the randomness in the resulting system. The system exhibiting the least randomness indicates the attribute that contributed the most randomness in the original setup.
The attribute that results in the least randomness is, therefore, a logical choice for a decision point in decision tree learning.
Section 1.3: The Bit-Based Explanation
Focusing on the term "Information Gain," it implies that some information is acquired. Information is quantified in bits.
Thus, we can also interpret information gain as the number of bits saved when the value of an attribute is known. A higher number of bits saved correlates with a greater information gain, which is advantageous for us.
Chapter 2: Limitations of Information Gain
Is the entropy reduction calculation for each attribute a reliable decision-making metric? Can it fail in certain scenarios?
Consider a situation where unique IDs are assigned to every user. If an ID is known, it reveals a person’s details, signifying a significant information gain. However, the flaw in using IDs as a decision point becomes apparent. Since IDs are unique, they only pertain to a single individual without uncovering broader data patterns. Consequently, information gain can be inadequate in specific instances. Future discussions will explore how to address this limitation, including concepts like information gain ratio.
Summary
In this article, we examined the concept of information gain from three different perspectives: mathematical, intuitive, and bit-based interpretations.
This video titled "Decision Tree 4: Information Gain" delves deeper into the mathematical aspects of information gain, offering a visual representation to enhance your understanding.
The video "Decision Tree - Entropy and Information Gain with Example" provides practical examples that illustrate how these concepts are applied in real-world scenarios.