Reducing Degrees of Freedom

When predicting how a physical system behaves, physicists often pose a vital question: how many degrees of freedom does this system possess? Degrees of freedom refer to the number of independent variables needed to completely describe a system's state. The term 'independent' is critical here; any quantity derivable from others does not count.

For instance, consider a particle in free space influenced by no external forces. In this scenario, we need three coordinates to pinpoint its exact location, indicating that its position encompasses three degrees of freedom. Conversely, for a bead constrained in a circular metal hoop, knowing just the angle suffices to locate it, leading to only one degree of freedom. This distinction is illustrated in the diagrams below.

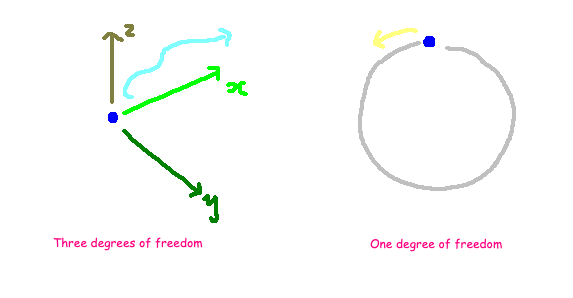
In more complex cases involving solid objects, determining orientation may necessitate three additional angles, thus resulting in six degrees of freedom instead of merely three. While the concept of degrees of freedom is relatively simple, identifying independent variables can be challenging. For instance, we might mistakenly consider momentum or energy as independent quantities, overlooking that they can be derived from others.

Our Universe as a Three-Dimensional Lattice

The holographic principle presents a radical viewpoint on the degrees of freedom of our universe. Conventional quantum field theory suggests that fields corresponding to particles and forces exist at every point in three-dimensional space. When these fields are excited, they produce particles. For example, at each spatial point, the electromagnetic field generates photons when excited.

Consequently, many physicists concur that fields in three-dimensional space describe our universe's degrees of freedom. It was previously believed that specifying these fields at every point was essential to fully characterize the universe's state at a given time. For instance, focusing on a point on your computer screen would require knowing various field values to understand the universe's dynamics at that location.

However, there’s a subtle flaw in this reasoning. Observations indicate that most physics is independent of phenomena occurring at the smallest scales, as evidenced by effects like the Casimir force. In previous discussions on renormalization, I noted that our observations often ignore microscopic details. For example, a comprehensive theory of fluid mechanics doesn't require knowledge of individual water molecules' behavior.

Thus, one might argue that we don't need to define a quantum field at every spatial point but only at sufficiently distant locations. Imagine our universe as somewhat pixelated; whether viewed through a high-resolution lens or a slightly pixelated one, we glean the same insights. Therefore, we need degrees of freedom only at points in a three-dimensional lattice, a structure with evenly spaced points.

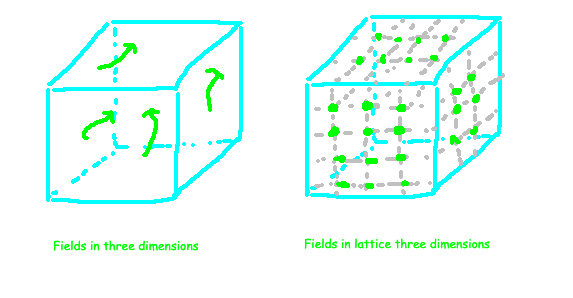
The diagram on the left depicts fields freely acting everywhere in space, whereas the one on the right illustrates our current understanding of the universe as a slightly coarse lattice structure.

The Holographic Principle

The holographic principle simplifies the reduction of our degrees of freedom to an astonishing degree. It asserts that the degrees of freedom in our universe can be fully encoded on a two-dimensional lattice.

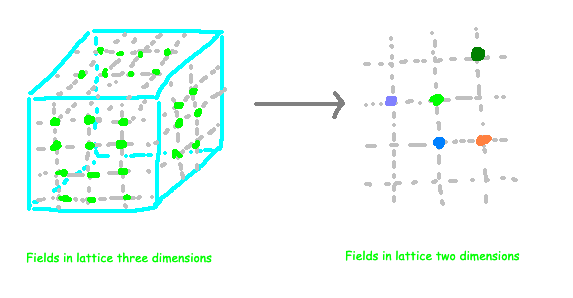
The above diagram reflects a shift in our conceptual framework. Initially, it was believed that three dimensions were necessary to encapsulate the universe's state, but now we are questioning whether two dimensions suffice.

The best analogy to convey this principle involves projecting onto a movie screen. The holographic principle suggests that physicists can derive all information about our three-dimensional universe from a projection on a two-dimensional boundary. For instance, the diagram below illustrates a black hole being projected onto a cinema screen, representing our two-dimensional boundary.

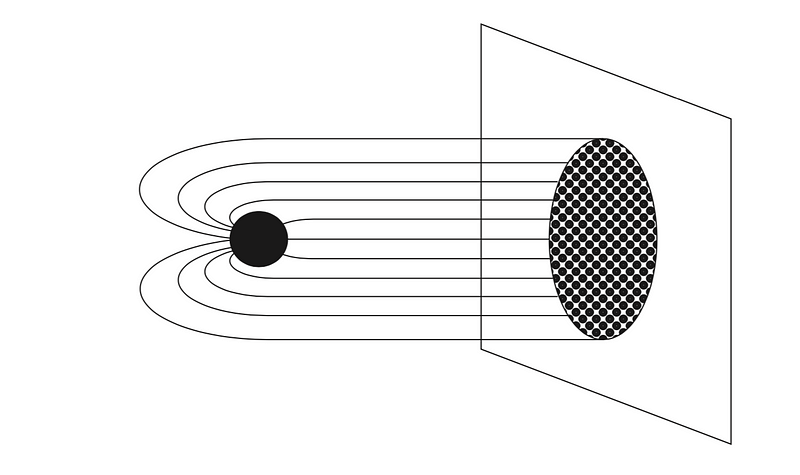
Susskind's illustration demonstrates a black hole's projection onto two-dimensional space. t' Hooft argues that all information within a system can be encoded on a distant two-dimensional boundary. L. Susskind, The World as a Hologram, arXiv:hep-th/9409089

Although the holographic principle remains largely theoretical, what physics necessitated such a radical idea? To explore this, we must examine black holes and their thermodynamic properties.

The Black Hole Argument for the Holographic Principle

Entropy, a measure of disorder in a system with numerous particles, plays a crucial role in physics. In essence, it reflects the total number of possible configurations a particle system can occupy. When studying extensive systems, physicists typically adopt a statistical approach, as individually modeling numerous particle interactions is overly complex. For a large number of particles, the goal is to count all potential states and their probabilities. When probabilities are widely distributed, indicating high uncertainty about a system's state, we classify that system as having high entropy.

The formula for entropy in a simplified model is expressed below. Here, S represents entropy, and the Greek letter omega signifies the total number of states a system can occupy.

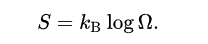
Consider hot gas—it possesses high entropy due to numerous particles bouncing around, resulting in relatively low certainty regarding any specific state. This contrasts with a block of ice, where each particle is fixed within the lattice.

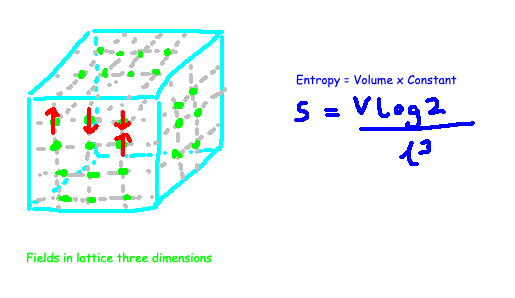
We can compute the entropy for a basic toy model. In a three-dimensional cubic lattice where individual atoms can occupy either an up or down spin, the entropy scales in proportion to the cube's volume. This scaling law, which states that entropy increases with system volume, appears applicable to all objects. However, it doesn't hold true for black holes.

Black holes are astronomical entities with a tremendous gravitational pull, preventing anything, including light, from escaping. Initially, Einstein's theory of relativity predicted their existence, but it has little to say about large particle systems. Consequently, scientists previously believed black holes lacked entropy; they were viewed as cold, massive structures devoid of thermal quantum physics.

According to the second law of thermodynamics, the entropy of an isolated system can never decrease. However, the fact that black holes consume all matter presents a significant philosophical dilemma. If one were to position a highly entropic hot gas near a black hole, it would be drawn in, causing the total entropy of our system to diminish! This loss of entropy would directly contravene the second law.

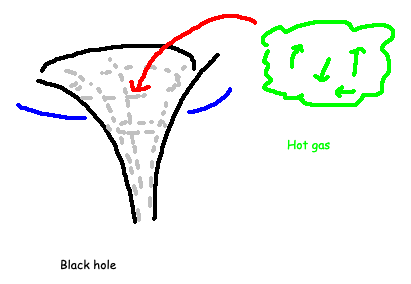
The only resolution was to assert that black holes must possess entropy. Bekenstein demonstrated that for the second law of thermodynamics to hold, black holes must have immense entropy, surpassing that of any other objects in the universe. He derived an upper limit for black hole entropy, which turned out to be proportional to the area, not the volume, of the black hole!

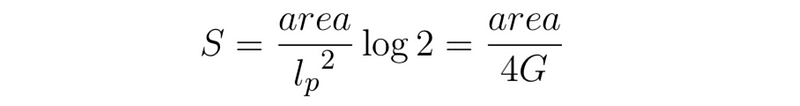
The formula for black hole entropy illustrates that it is dependent on its area, not its volume. This suggests that the information contained in a black hole resides in its boundary—a two-dimensional structure—rather than its volume. This revelation served as a key motivation behind the holographic principle. Thus, we have a quantity, entropy, that no longer considers the entire volume of an object, but rather its boundary.