The Crucial Role of Feature Scaling in Unsupervised Learning
Written on
Chapter 1: Introduction to Feature Scaling
Understanding the importance of feature scaling is essential when developing unsupervised learning models. This is especially true for clustering or segmenting data points, where ensuring accurate results is paramount. Neglecting feature scaling before utilizing models like k-means or DBSCAN can lead to skewed or invalid results. In this discussion, we will delve into the reasons behind this necessity, along with illustrative examples.
Section 1.1: What is Unsupervised Learning?
Unsupervised learning refers to a category of machine learning algorithms that can categorize, group, and cluster data without requiring explicit labels or target variables. This approach is beneficial for tasks such as customer segmentation in marketing or grouping similar properties in real estate models. The key takeaway is that it identifies patterns among different groups without needing predefined labels, allowing for self-directed analysis of outputs to extract meaningful insights.
Section 1.2: Defining Feature Scaling
Feature scaling encompasses various statistical methods that adjust the scales of features in our data to ensure a uniform range. To illustrate, consider a dataset containing information about bank clients' account balances, ranging from $0 to $1,000,000, alongside their ages, which vary from 18 to 100. By applying a feature scaling technique, we can standardize both features to a common range, such as 0 to 1 or -1 to 1.
Main Feature Scaling Techniques
The primary techniques for feature scaling are Normalization and Standardization.
- Normalization adjusts feature values to a specified range (commonly 0 to 1), irrespective of their statistical distributions. It utilizes the minimum and maximum values of each feature, making it somewhat sensitive to outliers.
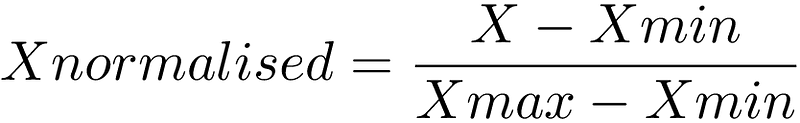
- Standardization transforms data to follow a normal distribution, typically with a mean of 0 and a standard deviation of 1. This technique is preferable when data is known to conform to a standard distribution or when outliers are present.
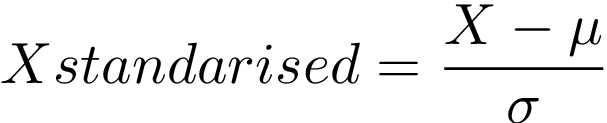
Section 1.3: The Importance of Feature Scaling
Feature scaling plays a critical role in machine learning algorithms that rely on distance metrics, such as clustering methods like k-means. These metrics aggregate calculations across individual features into a singular numerical value that serves as a similarity measure. A well-known distance metric is the Euclidean distance, which is calculated as follows:
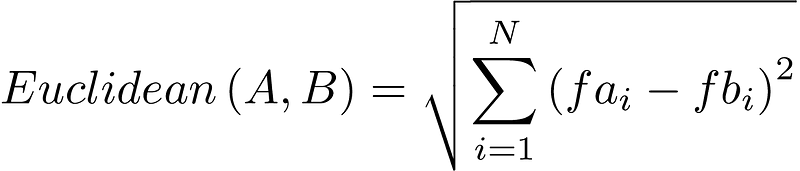
This formula indicates that the Euclidean distance computes the squared differences of each feature between two data points, sums them, and then takes the square root. Consider the following two data points for analysis:
- Data Point A: $125,000 bank deposit, age 52
- Data Point B: $100,000 bank deposit, age 45
In this scenario, the contribution of the bank deposit feature to the Euclidean distance significantly overshadows that of the age feature. This discrepancy arises not from the inherent importance of the features but rather from the vast difference in their value ranges. By employing a feature scaling technique, both features can be normalized to the same range, thereby mitigating issues of dominance.
Chapter 2: Practical Example – Weight and Height
To further illustrate the significance of feature scaling, let’s consider a dataset containing the weights and heights of 1,000 individuals. Heights are measured in meters (approximately ranging from 1.4m to 2m), while weights are recorded in kilograms (from around 40 to over 120 kg). The following scatter plot represents this data:
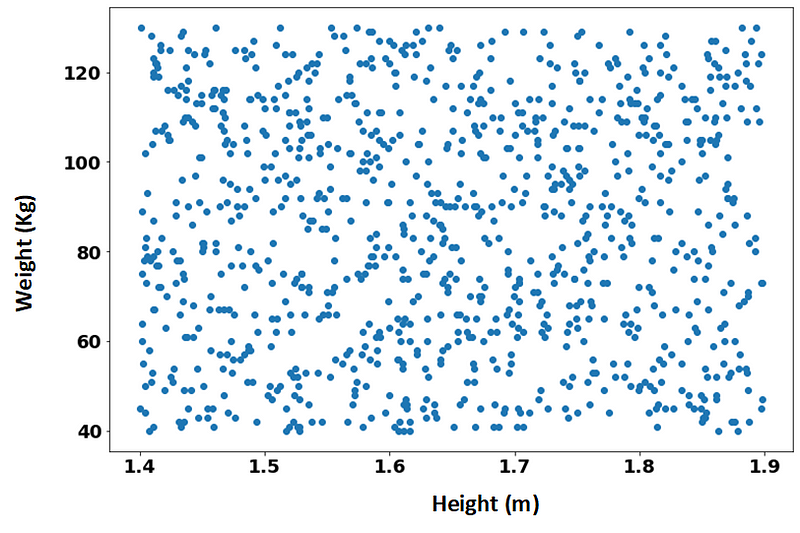
In this example, weight exhibits a far greater range than height. Assume our goal is to segment the data into four clusters based on:
- Low weight, low height
- Low weight, tall
- High weight, low height
- High weight, tall
To achieve this, we can employ a k-means clustering algorithm that calculates Euclidean distances to form these clusters. The resulting clusters appear as follows, with each color denoting a distinct group:
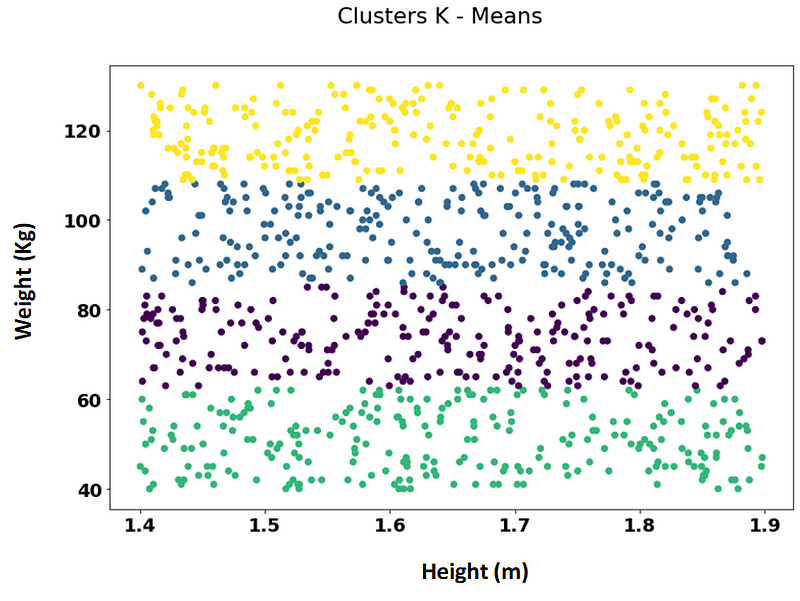
Here, it becomes evident that the clusters are predominantly influenced by weight, as height has little to no effect on the segmentation. To rectify this situation, we apply a feature scaling technique, such as standardization, to our dataset:
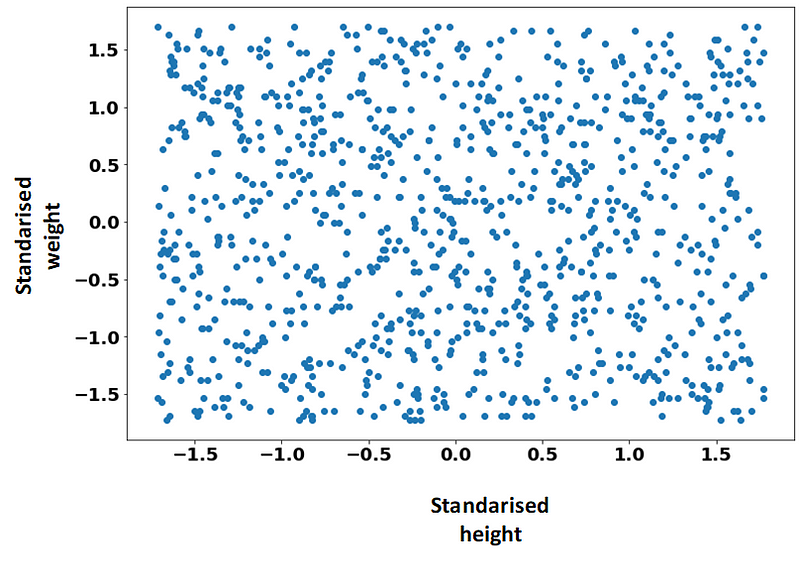
Now, both weight and height are confined within a similar range of -1.5 to 1.5, devoid of any specific units. We can now reapply the clustering algorithm to these standardized features.
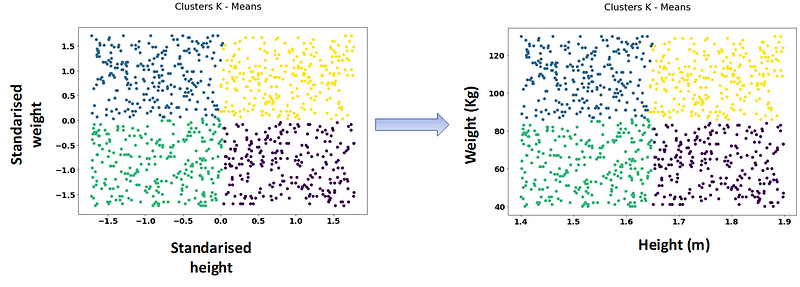
The left scatter plot illustrates the k-means clustering based on standardized features, while the right plot shows how these clusters translate back to our original data points. As a result, we can now clearly identify the four intended groups, effectively segmenting individuals according to their height and weight.
Closing Thoughts and Further Resources
In conclusion, I hope this discussion has shed light on the critical importance of feature scaling in machine learning. For those interested in exploring this topic further, I recommend the following resources:
- Distance Metrics in Machine Learning
- Feature Scaling in Machine Learning: Understanding Normalization vs. Standardization
- Machine Learning Mastery: Rescaling Data for Machine Learning in Python
Additionally, feel free to explore this repository for more insights on machine learning and AI!
This video explains why feature scaling is essential in machine learning models, providing clear examples and insights.
A detailed discussion on the necessity of feature scaling, highlighting its impact on model performance and accuracy.