Exploring the Lessons Springs Offer About Solids
Written on
Chapter 1: The Nature of Solids
When considering solids, one might envision them as rigid entities with atoms stuck in fixed positions. However, the reality is that atoms within solids are in constant motion, much like those in gases. The crucial distinction lies in the fact that, in solids, atoms do not shift in relation to their neighbors. They maintain a structured arrangement—such as the hexagonal configuration, where each atom has six immediate neighbors—which is vital for the unique characteristics that set solids apart from other forms of matter.
Why do atoms in solids bond together while those in gases do not? At the atomic level, two primary forms of energy come into play: thermal energy and energy from electrical interactions among atoms. While this explanation simplifies the complexity of atomic interactions, other forces, including electron configurations, magnetic fields due to charge movements, and nuclear energies, also contribute. A comprehensive understanding of these factors and their impact on material properties involves the principles of quantum mechanics. For now, however, we can set aside these intricate interactions and focus on the fundamental question: what causes atoms in a solid to adhere to one another?
The answer is relatively simple. When thermal energy is elevated, atoms are agitated and move about freely. Conversely, as temperature decreases, thermal energy diminishes, allowing atoms to become more aware of their interactions with neighboring atoms. At sufficiently low temperatures, these atomic interactions dominate, leading to the formation of a solid as atoms cluster together and crystallize.
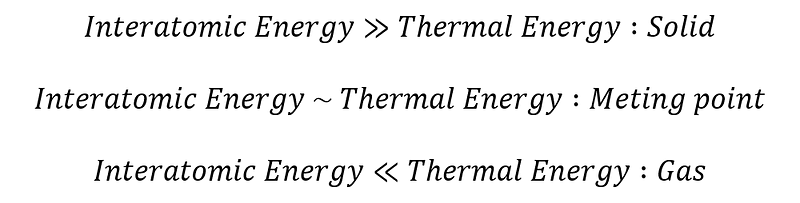
Understanding Energy Contributions
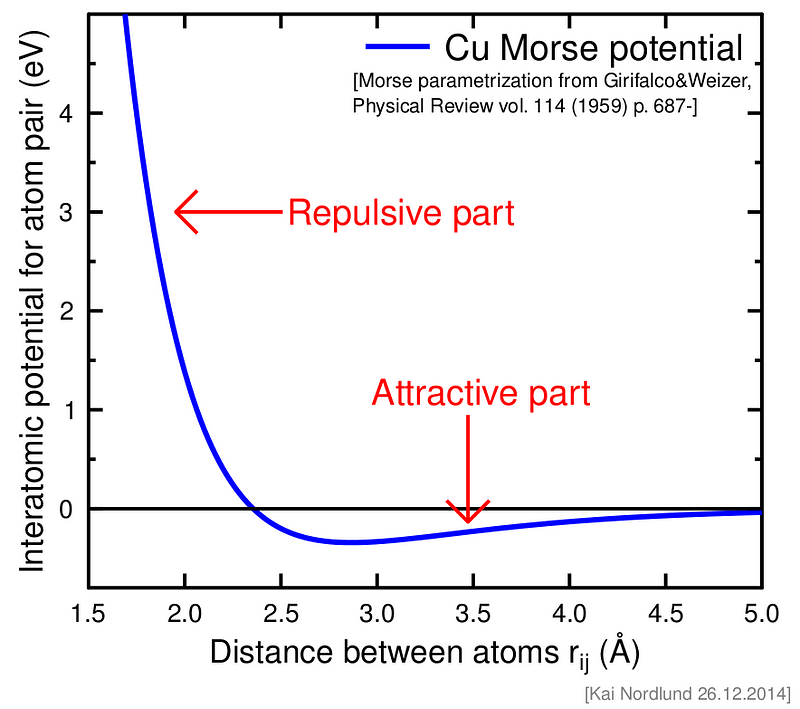
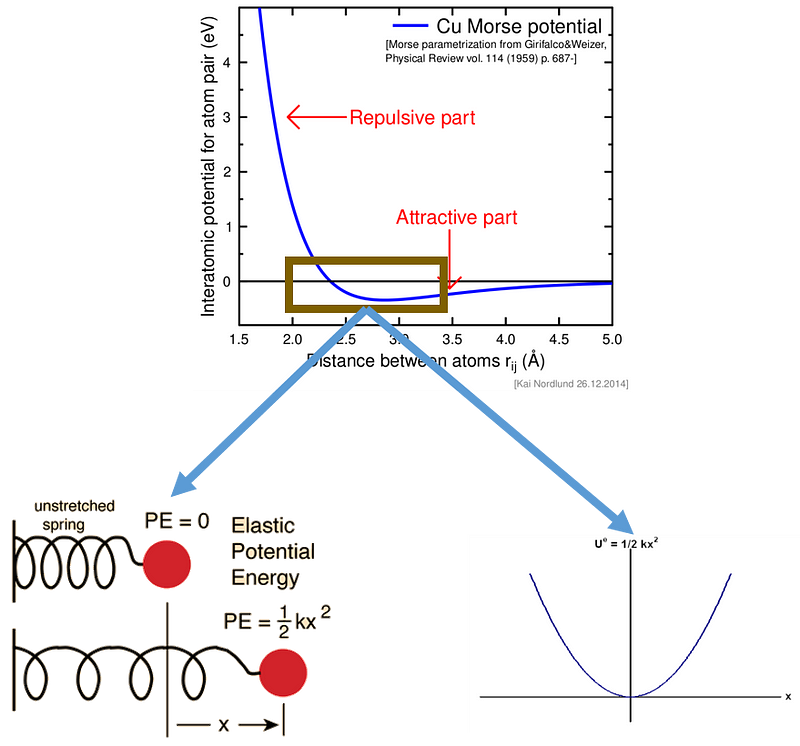
In the graph depicting the interaction potential of Copper (Cu), the y-axis represents energy measured in electron volts, while the x-axis indicates the distance between atoms in Angstroms. When the distance between atoms drops below approximately 3.5 Angstroms, they begin to experience a negative potential, signifying a preference for bonding. The most attractive potential occurs at around 2.6 Angstroms, with a value of roughly -0.5 eV. Beyond this distance, Copper atoms start to repel one another due to positive potential.
At room temperature, thermal energy, quantified as kT (with k being the Boltzmann constant), equals about 0.026 eV, which is significantly less than the maximum attractive energy experienced by Copper atoms (-0.5 eV). This indicates that Copper remains solid at room temperature, as the interatomic energy greatly surpasses thermal energy. However, at Copper's melting point of 1358 K (1984 F), thermal energy rises to 0.12 eV, nearing the minimum energy of attraction between Copper atoms (-0.5 eV), resulting in the transition to a liquid state.
The Connection Between Solids and Springs
Now that we grasp why solids form at lower temperatures, let’s explore what defines their characteristics. The most notable property of a solid is its elasticity, which can be understood through the interactions of its atoms. This concept may seem complex, but physics often simplifies intricate problems. One common approach is to model atoms as spheres and their interactions as springs, a foundational concept in physics.
The spring potential energy is expressed as 1/2kx², where x denotes the displacement from the equilibrium position and k represents the spring constant. When a spring is compressed or stretched, it generates potential energy that urges it back to its equilibrium state. Similarly, atoms positioned about 2.6 Angstroms apart exhibit spring-like interaction potentials; stretching them leads to a tendency to recoil, which is the essence of elasticity. Yet, this analogy alone is insufficient, and we will delve deeper into how elasticity arises from atomic springs.
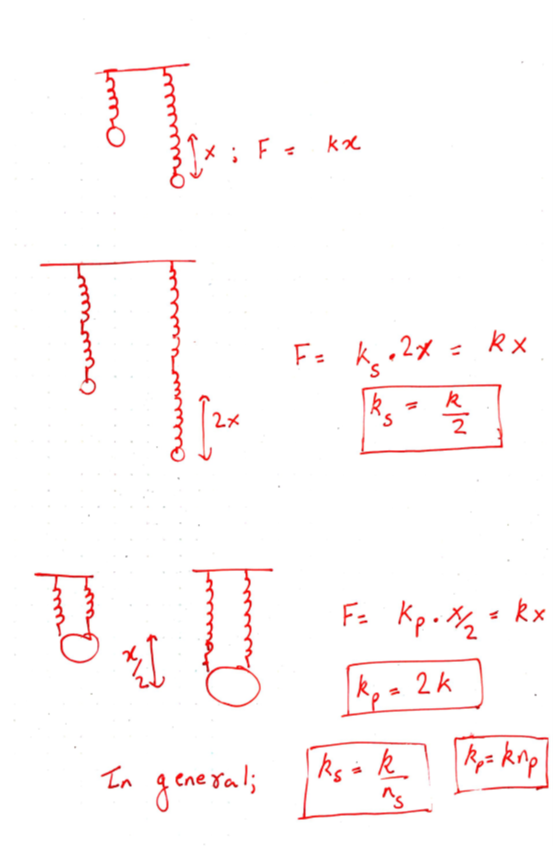
Exploring Multiple Springs
A spring has a specific spring constant k, which indicates the force needed to displace it according to Hooke’s law. A higher spring constant means a greater force is required for displacement, resulting in a stiffer spring, while a lower spring constant indicates a softer spring.
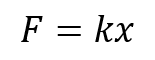
What occurs when multiple springs are linked together?
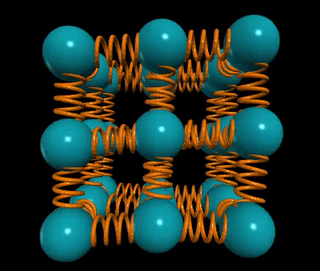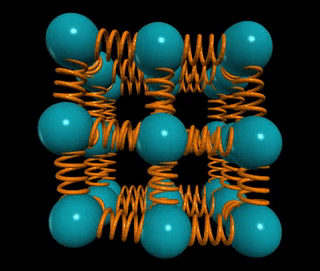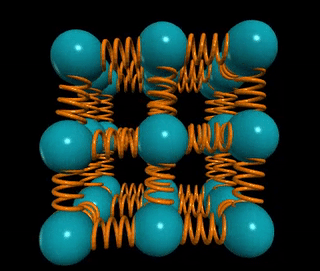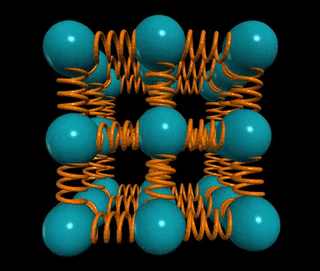
Let’s visualize a solid wire of length L and cross-sectional area A. How does the material's stiffness vary with changes in A versus L?
When two springs are connected in series, as in the example of two chewing gum sticks, pulling them apart becomes easier. In this configuration, the effective spring constant becomes ks = k/2. Conversely, if those two springs are joined in parallel, as if glued together, they become stiffer, with the spring constant becoming kp = 2k.

In general, for n springs in series, the spring constant is k/n, while for n springs in parallel, it is k*n. This concept applies to solids as well: if the distance between atomic springs is d, then the number of springs in series across a solid of length L is ns = L/d, and the number of springs in parallel is np = A/d².
Understanding Elasticity from Atomic Springs
We now have a formula for the overall spring constant of solids in relation to the atomic spring constant k and the distance between atomic springs d. But how does this connect to elasticity? Elasticity is defined as Stress/Strain, where Stress is the force applied per unit area, measured in Pascals, and Strain refers to the deformation of the solid relative to its original length.
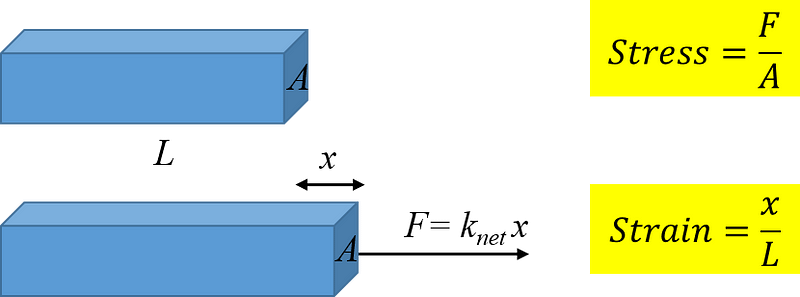
By substituting the variables, we arrive at elasticity as k/d—the ratio of the interatomic spring constant to the distance separating the springs. This relationship clarifies that elasticity is a familiar concept: rubber bands are elastic, and while one might not consider an iron rod elastic, it indeed is, albeit significantly stiffer and harder to stretch. This discussion illustrates how the stretching of a solid directly correlates with atomic interactions occurring at a scale billions of times smaller.
If you enjoyed this exploration into how macroscopic properties arise from atomic interactions at suitable scales, consider following the Emergent Phenomena publication. We delve into how complex everyday phenomena, from materials to societal structures, develop from fundamental principles.