Triangle Symmetries

To grasp the upcoming concepts, we will begin with the symmetries of a triangle, refining our definitions from basic geometry.

Definition 1 - Triangle: A triangle consists of three distinct points on a plane or the area enclosed by three unique lines in that plane.

Definition 2 - Equilateral Triangle: An equilateral triangle has all three sides of equal length.

From basic geometry, we also know that the internal angles are equal. Euclid's method for constructing an equilateral triangle is as follows:

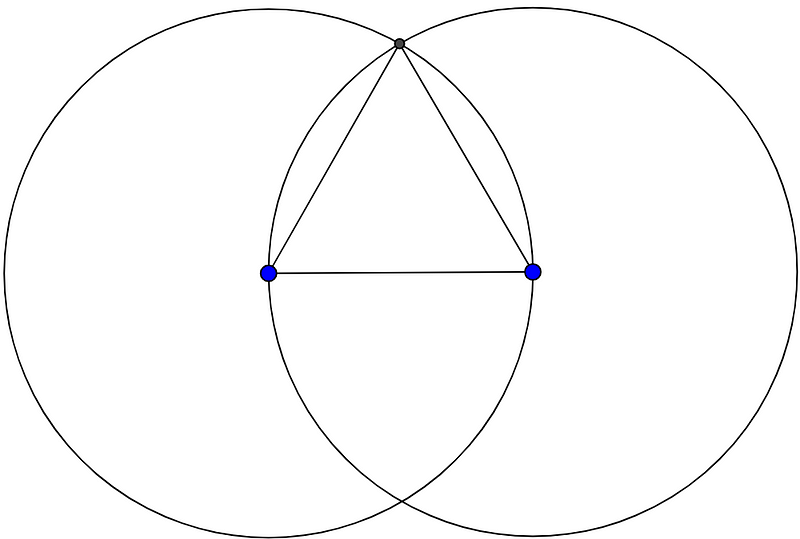
Since both circles share a common radius, and all three points lie on both circles, the distance between any two points must be identical. This will be elaborated upon later; so keep that in mind!

Now, the question of triangle symmetries is essentially: "What modifications can we apply to the triangle that would result in an indistinguishable copy of the original?"

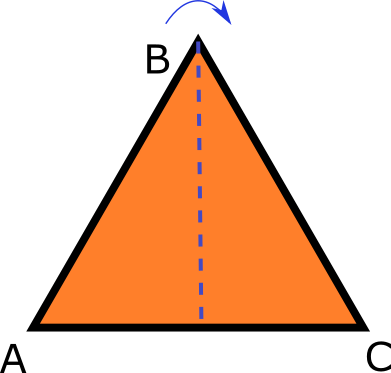
Consider triangle ABC depicted here. We can reflect it across one of its bisectors or rotate it by one-third of a full turn. We will denote these transformations as r for rotation and f for reflection, and we will express them based on their effects on the triangle’s vertices:

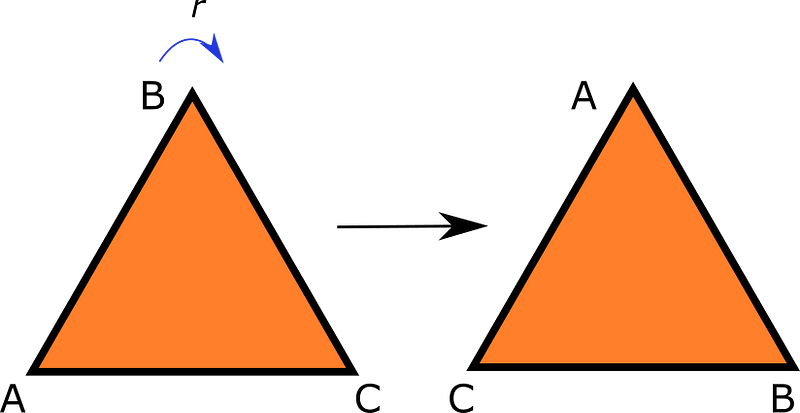
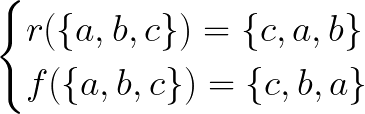
By performing these operations, we discover that there are six distinct outcomes, formed by combining rotations and reflections. For example:

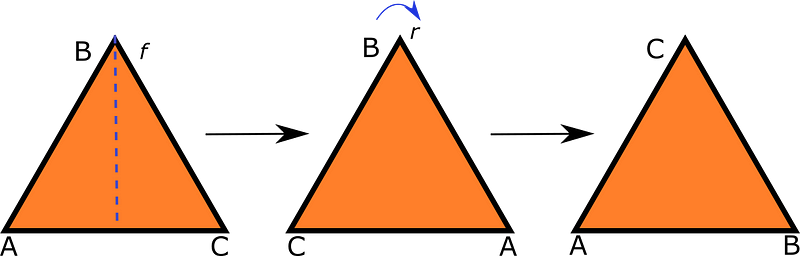
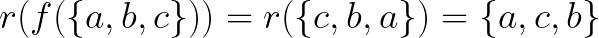
This leads us to conclude that the triangle {a, b, c} has a set of rotations and reflections that keep it invariant; these transformations are derived from a single rotation and a single reflection.

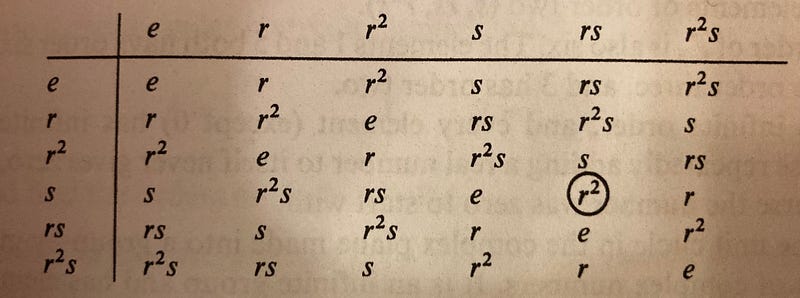
These transformations are referred to as symmetries, although this definition is still somewhat preliminary. We will denote the triangle along with these symmetries as (T, G), where

T = {a, b, c} and G = (r, f, r², rf, r²f). This notation describes the characteristics of an equilateral triangle: it consists of three points, and specific rotations and reflections (contained in G) leave it unchanged. For now, we will continue to call these symmetries while refining our definition later.

Groups: Understanding Their Significance

Definition 3 - Group: A group is a set X, paired with a multiplication operation (denoted ab for the product of a and b) that satisfies:

• X is closed: no element of X can be produced outside of X through multiplication.
• X has an identity element: there exists an element e such that for any x in X, ex = xe = x.
• The multiplication operation is associative: a(bc) = (ab)c = abc for all a, b, c in X.
• Each element has an inverse: for every x in X, there exists an element y such that xy = yx = e, with this y represented as x^(-1).

A group is essentially any collection of elements that adheres to these criteria. Referring back to our triangle example, G, as outlined above, qualifies as a group. When the various rotations and reflections are combined, the result is another rotation or reflection; it includes an identity element, and as our table indicates, each rotation or reflection has an inverse. Lastly, it is associative, as one can verify through similar reasoning.

It is crucial to note that the triangle itself does not constitute the group, nor do the vertices; rather, the set {a, b, c} is being acted upon by the group of rotations and reflections. This group is known as D3, the dihedral group acting on three objects.

Before we proceed, take a moment to breathe and avoid overcomplicating things. So far, we have merely labeled concepts that we already have an intuitive grasp of. The significant leap is in separating these symmetries from the objects they relate to, which is a valuable insight that will become apparent.

# Examples and Insights

Arithmetic Modulo 3

Let's explore two additional straightforward examples of groups, beginning with a clock that has three hours:

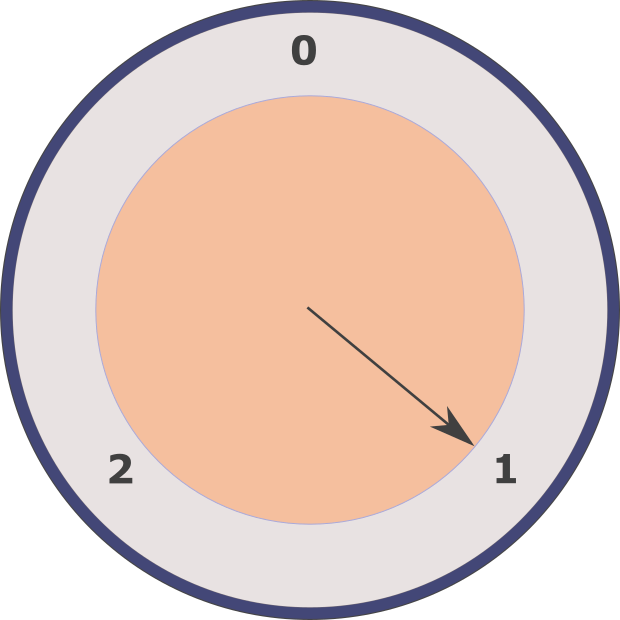
On this clock, we will establish basic arithmetic. For instance, 2 + 1 results in 0, as one hour after 2 is 0. Thus, 2 + 1 = 0.

Similarly, 2 + 2 = 1, and 2 x 2 = 1. All other operations behave as expected.

This arithmetic is referred to as modulo 3. We will concentrate on the addition properties for now; under this addition operation, we label the set {0, 1, 2} as Z3, and we perform addition within it. This is a very basic group acting on this simple set. An excellent exercise for interested readers would be to verify that this scenario (Z3, +) constitutes a group.

This also corresponds to the group formed solely by the rotations of the triangle.

The Rational Numbers

Consider any fraction p/q, where p and q are both non-zero. Under multiplication, this forms a group. Interestingly, they also form a group under addition, where 0 is permitted for p (but not for q! Note: the identities are 1 for multiplication and 0 for addition).

Rotations of the Unit Circle

You may have noticed that rotations easily yield groups in the plane (more on this later). The set of all rotations acting on either the plane or any circle centered at the origin also forms groups. (Try verifying this!)

Group Properties

Now that we have a few examples, let’s discuss some essential terms and concepts:

• Abelian: A group is called abelian if the operation is commutative, meaning xy = yx for all elements in X.
• Subgroups: If a subset of the group remains a group under the same operation, it is termed a subgroup. A notable example is the integers under addition and any collection of multiples of primes; e.g., {...-10, -5, 0, 5, 10, 15...} represented as 5Z (not to be confused with Z5!).
• Group Order: The number of elements within a group is referred to as its order.
• Lagrange’s Theorem: If H is a finite order group and G is a subgroup of H, then the order of G divides the order of H (this leads to various interesting theorems in number theory!).
• Element Order: The order of an element g is the smallest integer k such that g^k = e, where e is the identity.
• Cauchy’s Theorem: If H is a finite order group n, and p is a prime that divides n, then H contains at least one element of order p.

These concepts provide frameworks to consider groups as underlying structures in number theory and geometry, leading us to our final definition, which should clarify much of our terminology.

Geometry Through the Lens of Groups

Definition 4 - Geometry: A geometry is represented as a pair (S, G), where S is a set and G is a group of transformations.

Definition 5 - Transformation: A transformation is defined as a function T from a set A to itself, typically expressed as T: A ? A, such that each element in A maps uniquely to another element in A (injective) and every element in A is covered by the output of T (surjective). A function that is both one-to-one and onto is called a bijection, and a bijection from a set to itself (preserving the group structure/action) is termed an automorphism.

Thus, a geometry can be viewed as a set accompanied by a group of functions that map onto itself, or as a set with its group of automorphisms, often referred to as symmetries.

Returning to our triangle, we can utilize the language we have developed to gain insights:

Now, let’s apply our newfound terminology!

In this context, the entire geometry is represented as (S, G). The triangle serves as the set S = {a, b, c}, with the automorphism group consisting of combinations of r and f (which we say is generated by them). We denote this group as either G or as <r, f>.

The elements r and f have orders of 3 and 2, respectively, since r³ rotates the triangle in a cycle (a ? b ? c ? a), while f² reflects it (a ? c ? a, leaving b unchanged). The combinations of r and f constitute the triangle's symmetries.

Finally, we arrive at a crucial definition:

Definition 6 - Euclidean Geometry: Euclidean geometry is defined as the set C of complex numbers, paired with the group H of transformations in the form T(z) = r(z) + b, where z represents a complex number and b is a complex constant.

This represents all rotations and translations of the plane. See if you can grasp why this definition is sensible, and I will provide links to resources that delve deeper into this connection. This exploration is a powerful tool.

Feel free to leave comments if you'd like me to cover other mathematical topics!

Resources/Further Reading:

Geometry and Cosmic Topology by Michael Hitchman: https://mphitchman.com/geometry/gct-toc.html

Groups and Symmetry by M.A. Armstrong: http://chiataimakro.vicp.cc:8880/Mathematics/%E6%95%99%E6%9D%90/UTM-Undergraduate%20Texts%20in%20Mathematics/UTM%20Armstrong%20%20groups%20and%20symmetry.pdf