Discovering the Wonders of Pi: 20+ Amazing Insights
Written on

At last, the weekend had arrived! After delivering a lengthy presentation on mathematics, I returned home to unwind with my favorite show, Person of Interest. To my surprise, the episode revolved around the renowned mathematical constant, pi (?), defined as the ratio of a circle’s circumference to its diameter, typically approximated as 3.14159. The character Mr. Finch took on the role of a substitute teacher and wrote 3.1415926535 on the chalkboard, prompting the students with the question, “What does this signify?”
In my mind, I knew the answer: “If I have a bicycle tire with a diameter of 1, then one complete rotation of the tire would cover a distance equal to pi.” Yet, no one in the show responded. Mr. Finch then answered his own question:
> Pi, the ratio of the circumference of a circle to its diameter — 3.1415926535 — is merely the beginning. This sequence of digits continues infinitely without repetition, meaning that hidden within is every conceivable number; your birth date, the combination to your locker, your social security number, and more. Everything is encoded within this numerical string. Furthermore, if you translate these digits into letters, you could recreate every word in every conceivable permutation; from the first syllable you uttered as a child to the name of your latest crush, even your entire life story. The infinite possibilities of the universe rest within this simple circle. What will you do with this knowledge? That’s for you to determine!
While the scene may not have been entirely accurate, I found it captivating. This portrayal is striking because many educators aspire to be as engaging and witty as Mr. Finch. His deep understanding of the subject matter elevates the discussion beyond textbooks and keeps students attentive throughout the lesson.



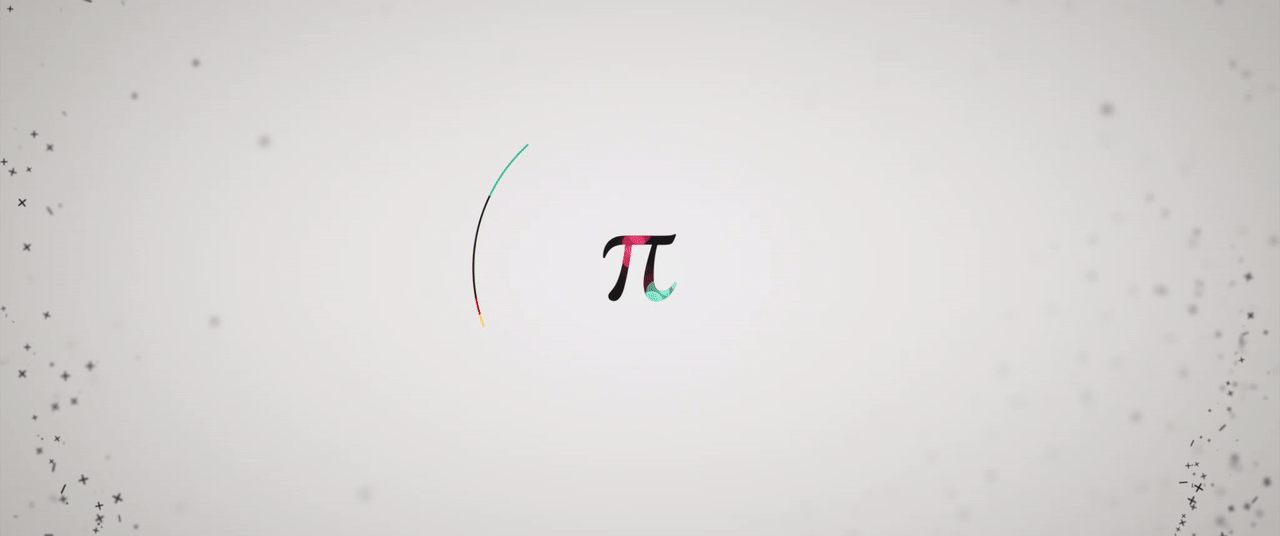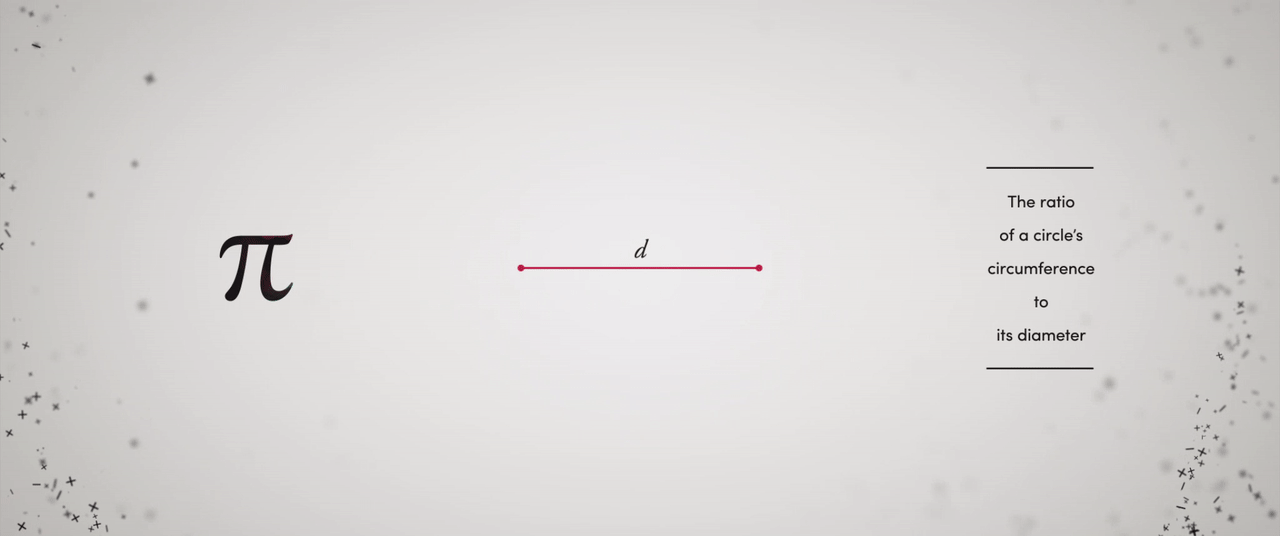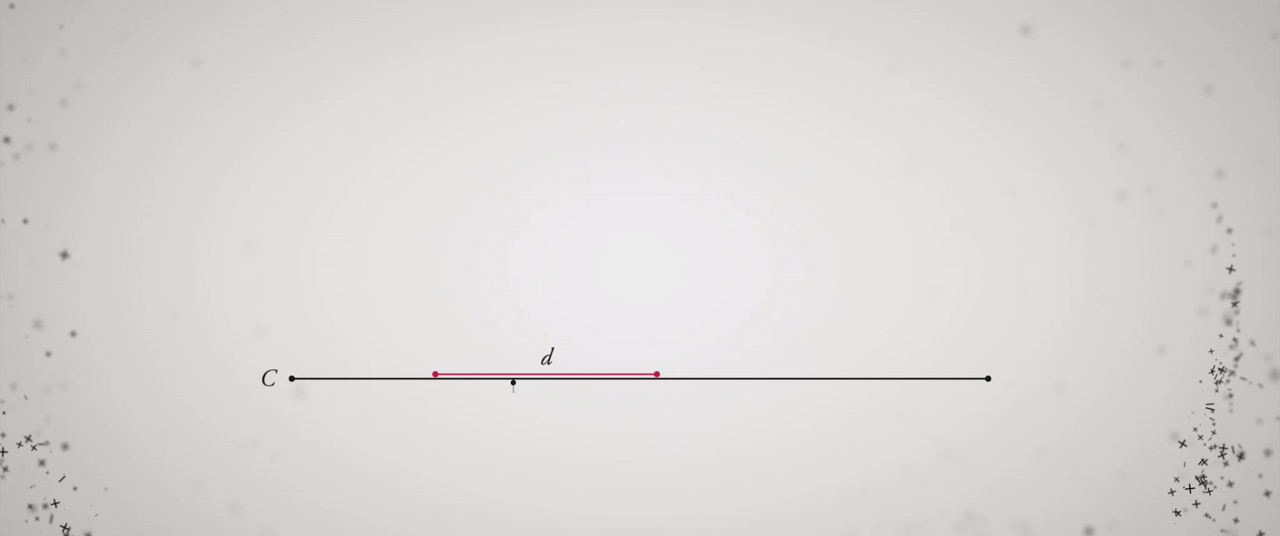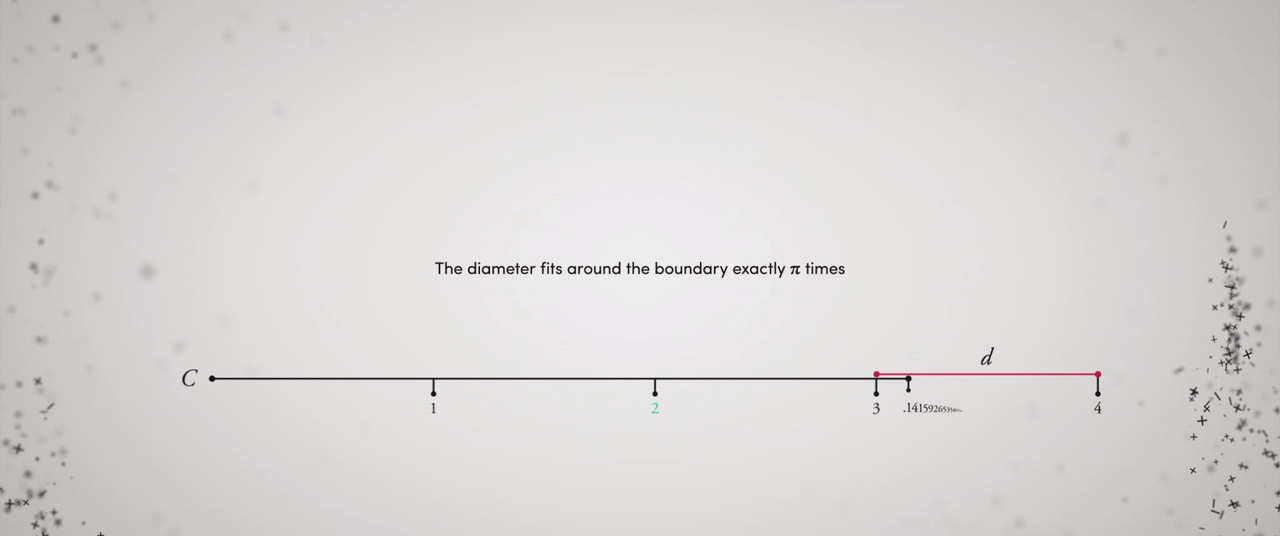
> Unfortunately, Mr. Finch's assertion was flawed since mathematicians have yet to prove whether pi exhibits the property of “normality.” In simpler terms, they remain uncertain if ? includes every possible finite arrangement of digits from 0 to 9. They do not know if each digit appears an infinite number of times in pi's decimal representation.

Pi as a Random Number Generator
No one knows what we might discover in the digits of ? as we continue to calculate. For example, in examining the first billion digits of ?, the digit 7 appears nearly 100 million times. This statistical occurrence makes ? an excellent random number generator since the probability of landing on 7 should be 1/10 or 10%.
However, at some points, ? might not include the digit 7 and could instead display a non-repeating sequence with just a few digits, such as 010203112233000111222333... For instance, after the initial 761 digits of ?, a notable mathematical coincidence occurs, known as the Feynman point, where six nines appear consecutively.

Understanding Pi's Transcendental Nature
In 1882, Ferdinand Lindemann established that ? is a transcendental number, meaning it cannot be expressed as a solution to any non-constant polynomial equation with rational coefficients.
The Randomness of Pi
It is certain that the digits of ? extend infinitely and in a random sequence. This randomness is intriguing because while the value of ? is finite, its decimal representation is endlessly long. This may seem contradictory, but it is not. The constant ? is defined as the ratio of a circle’s circumference to its diameter, both finite quantities. Yet, we still seek an approximate value for ?.
In 1768, Johann Lambert proved that the value of ? is an irrational number, meaning it cannot be expressed as a simple fraction. The approximation 22/7 is commonly used, but it does not encompass all the digits of ?. This is because irrational numbers extend infinitely without following a predictable pattern.
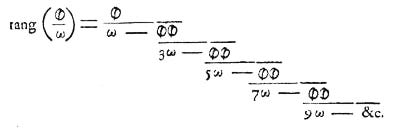
Mathematician Yasumasa Kanada demonstrated that the first trillion digits of ? appear statistically random, requiring over 600 hours for the calculations. In the table below, you can observe the occurrence of each digit, where the probability remains one-tenth for each.
Digit Occurrences 0 99,999,948,134 1 99,999,945,664 2 100,000,480,057 3 99,999,787,805 4 100,000,357,857 5 99,999,671,008 6 99,999,807,503 7 99,999,818,723 8 100,000,791,469 9 99,999,854,780 Total 1,000,000,000,000
After many years, Emma Haruka Iwao computed 34.1 trillion digits of ? in 2019, a task that took 121 days due to the immense computational power required. To visualize this, if you were to print a billion decimal places of ? in standard font size, it would stretch from New York to Kansas.
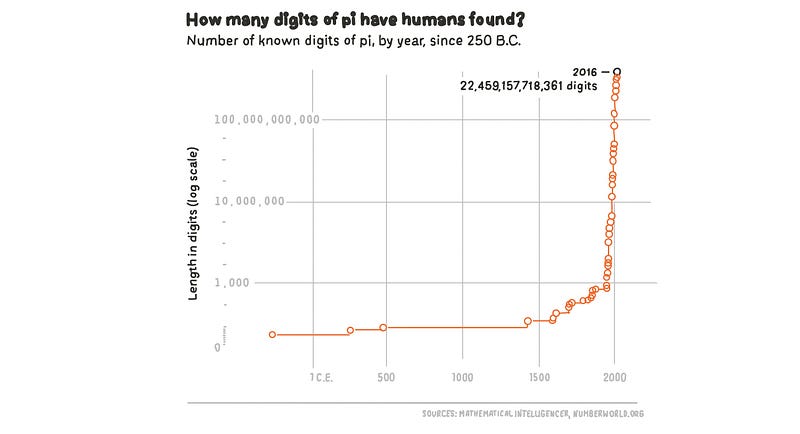
Yet, 34.1 trillion digits are still insufficient to ascertain whether ? is normal. Supercomputers continue to crunch the numbers. The graph below illustrates the number of known digits of pi over the years since 250 B.C.
Discovering Personal Significance in Pi
Returning to Mr. Finch's assertion, he isn't entirely mistaken. It is indeed possible to find our birthdays within the digits of ?. You can visit mypiday.com and enter your birth date to discover its specific decimal place in ?. For instance, my birthday is located at the 675,097th decimal place.
> If ? is a normal number, then it could be claimed that our entire destiny is encoded within its digits. The photographs we take are represented in ? because digital images consist of binary numbers. All digital artifacts have existed in ? for millennia, including this article. Moreover, the DNA of every organism is encoded in ?. Mr. Finch's theory may hold some truth, though we have yet to confirm it.
The Intersection of Pi and Art
There are many artistic ways to illustrate the randomness of ?. While some scientists may be satisfied with their mundane scatter plots, numerous artists utilize color for data visualization to effectively communicate with the public. One such artist, Martin Krzywinski, found beauty in the randomness of ? by assigning different colors to each digit. For example, he painted three as orange, one as red, and four as yellow. The resulting artwork is visually striking, yet upon close inspection, no discernible pattern emerges within the colors.


Pi: The Most Studied Number in Mathematics
Among the many fascinating aspects of ?, it holds the title of the most studied number in mathematical history. Countless individuals aspire to memorize its digits, unlike other irrational numbers, which often lead to frustration and chaos. Mathematicians have dedicated centuries to calculating ? with precision.

Should we halt our pursuit of more digits of ?, or continue striving for better approximations? Is it sufficient to consider ? as merely 3.14? Can we rely on 40 digits of ? to determine the circumference of the Milky Way galaxy with an error smaller than a proton's size? Are the first 152 digits adequate to estimate the observable universe’s circumference, which measures 93 billion light-years?
For years, hundreds of mathematicians have endeavored to uncover more digits of ?, akin to reaching for the moon and beyond. But why? Why do mathematicians persist in calculating even more digits? Is it because ? is fundamental to every circle?
The Global Showcase of Pi
The underlying rationale might seem obscure, but ? serves as a splendid source for generating random numbers. However, the actual motivation is that nations can demonstrate their technological prowess by calculating the trillions of digits of ?, which requires formidable computing power. For instance, in the Star Trek episode “Wolf in the Fold,” Spock thwarts an evil computer by commanding it to “compute to the last digit, the value of ?.” Requesting a computer to compute ? is referred to as a “stress test” and could potentially cause it to crash.
On September 12, 1962, John F. Kennedy delivered a speech regarding the space program, stating:
> "There is no strife, no prejudice, no national conflict in outer space as yet. Its hazards are hostile to us all. Its conquest deserves the best of all mankind, and its opportunity for peaceful cooperation may never come again. But why, some say, the moon? Why choose this as our goal? And they may well ask why climb the highest mountain? We choose to go to the moon. We choose to go to the moon in this decade and do the other things, not because they are easy, but because they are hard because that goal will serve to organize and measure the best of our energies and skills, because that challenge is one that we are willing to accept, one we are unwilling to postpone, and one which we intend to win, and the others, too."