How Quantum Field Theory Operates

At the heart of quantum field theory is a concept known as the matrix element, which essentially provides the probability of a specific scattering event occurring. For example, to determine the likelihood of an electron colliding with a positron, one must calculate the matrix element for that interaction. This involves summing all possible Feynman Diagrams, where each diagram corresponds to a mathematical expression. Thus, the process of adding these diagrams equates to aggregating mathematical values.

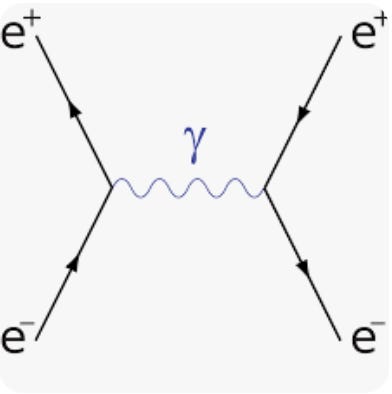
Despite the infinite number of Feynman diagrams possible for any given interaction, physicists like Sean Carroll reassure us that this does not lead to infinite results since higher-order diagrams contribute less significantly to the overall probability. This narrative is often the endpoint for most physicists, which explains the common belief in the elegance and success of quantum field theory. However, this explanation presented by Carroll is fundamentally flawed.

The Flaws in Quantum Field Theory

As one begins to add Feynman diagrams together, the results initially converge to a finite number—a positive sign. Yet, as higher-order diagrams are incorporated, the number of diagrams required explodes, leading to infinitely large results—a negative sign. To grasp this issue more clearly, we need to recognize that Feynman diagrams represent a perturbative series in mathematics. A series involves the successive addition of increasing quantities. For instance, the series 1 + 2 + 3 + 4... approaches infinity. This type of series is termed divergent. Conversely, some infinite series can converge to a single finite number, such as the Taylor Series.

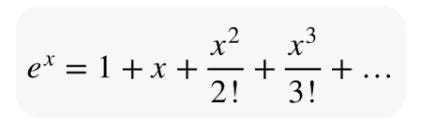
The series associated with Feynman diagrams is known as the Dyson Series. To find the probability of a scattering event, one sums all the terms in this series. The catch with the Dyson series is that it is asymptotic—initial terms converge accurately, but as more terms are added, divergence occurs. The first few terms yield results that are impressively accurate, aligning with experimental data up to eight decimal places. However, when one considers the entire series, the result trends toward infinity. Thus, when physicists claim quantum field theory provides ultra-accurate results, they refer to the limited initial terms of the Dyson series. It is crucial to acknowledge that the entire series diverges, leading to incorrect infinite outcomes. We are forced to truncate the series artificially, ignoring higher terms.

The situation deteriorates further when we explore other expressions such as cross sections and decay rates, which also rely on the matrix element. Since the matrix element is formally infinite, these quantities are rendered infinite as well. This suggests that quantum field theory posits an electron on one side of the galaxy has an infinite chance of colliding with a positron on the opposite side. Hence, the assertion that Quantum Field Theory is as successful as many claim is unfounded. This is not a hidden truth; it is well acknowledged among those scrutinizing the mathematical foundations of QFT. Even Richard Dyson himself argued in a publication that his series is asymptotic.

Nonperturbative QFT Solutions

So, have there been attempts to address these challenges? Indeed, efforts have been made! Since the core issue arises from the addition of terms in a questionable series, a potential solution involves abandoning the Dyson series entirely and seeking results via a non-perturbative approach. This gave rise to non-perturbative field theory, with Lattice Field Theory emerging as a leading candidate. This framework conceptualizes spacetime as a discrete lattice, resolving numerous mathematical issues inherent in conventional quantum field theory while ensuring expressions yield finite values.

But does lattice field theory completely resolve our concerns? Not entirely. While it effectively addresses quantum chromodynamics, the theory of strong interactions, it has yet to demonstrate efficacy for other field theories (it falls short for quantum electrodynamics), leaving the Standard Model still unrefined.

Conclusion

In summary, the Standard Model is arguably the most flawed theory created, as it produces incorrect infinite predictions. Only by arbitrarily halting the counting process can we retrieve accurate outcomes. Should we completely discard quantum field theory? Not necessarily. The inherent flaws do not render it a nonsensical theory. These issues may stem from the non-rigorous nature of perturbative QFT, and resolving these complications could lead to the elimination of these infinities. It is essential to clarify that scientists are not intentionally misleading anyone; many remain unaware of the foundational dilemmas within quantum field theory, and those who do sometimes struggle to communicate them effectively. I hope I have succeeded in conveying this complexity. For those interested in deepening their understanding of quantum field theory, consider visiting my channel, Fermion Physics. Thank you for reading, and until next time!

In the first video, "The Problem with Modern Physics with Sabine Hossenfelder," the discussion revolves around the fundamental issues plaguing current physics theories, particularly focusing on the shortcomings of quantum field theory.

The second video, "What is wrong with current physics | Eric Lerner, Sabine Hossenfelder, Roger Penrose, and more!" features insights from multiple experts addressing the inadequacies of modern physics frameworks.