Chapter 1: The Intricacies of Imaginary Numbers

When considering the square root of the imaginary unit ‘i’, most people might not find it particularly relevant. However, for those with a passion for mathematics, this inquiry can be quite captivating. It invites exploration and reveals new avenues for understanding.

The notion of the imaginary number ‘i’ is inherently complex. Adding the square root of i (√i) to the mix complicates things further. At first glance, this problem seems daunting. This article aims to demonstrate that this seemingly intricate question can be addressed more straightforwardly than one might expect, while also reinforcing fundamental concepts related to complex numbers.

Section 1.1: Imaginary Numbers and Their Origins

Imaginary numbers emerged to solve specific mathematical dilemmas. Historically, mathematicians encountered situations where they needed to find a number that squared to yield a negative result. Since no such real number existed, they conceptualized a new type of number, represented by ‘i’, which is defined as the square root of -1 (i = √(-1)).

An imaginary number can thus be viewed as a real number multiplied by the imaginary unit (i). The term “imaginary numbers” was originally used pejoratively by René Descartes, but later mathematicians like Leonhard Euler, Augustin-Louis Cauchy, and Carl Friedrich Gauss demonstrated their significant utility, leading to their widespread acceptance in mathematics.

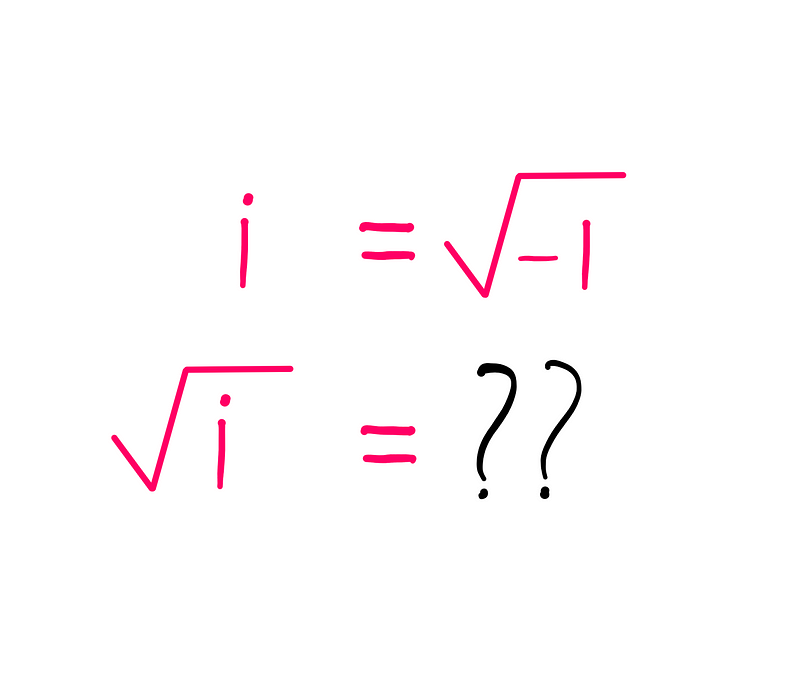
In modern mathematics, imaginary numbers play crucial roles in various applications.

Section 1.2: The Structure of Complex Numbers

Mathematicians recognized that imaginary numbers gain practical value when combined with real numbers, forming expressions like [x + (i*y)], where x and y are real numbers and i is the imaginary unit.

Visualizing these complex numbers on a Cartesian plane, the real numbers lie along the X-axis and the imaginary numbers on the Y-axis, creating what’s known as the complex plane.

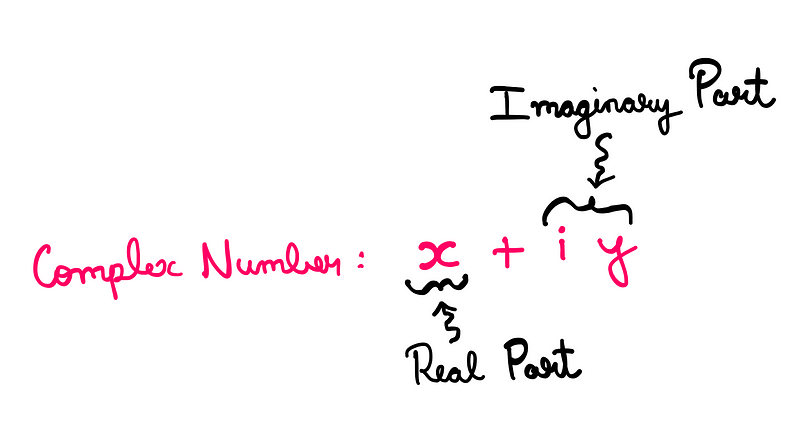
With this foundational understanding, we can now tackle the calculation of √i using both mathematical and intuitive approaches.

Chapter 2: Approaching the Square Root of i

To begin, we must acknowledge that any real or imaginary number can be expressed as a complex number. For instance, the imaginary unit i can be represented as:

i = x + iy

where x = 0 and y = 1, leading to i = 0 + (1*i).

Thus, we can express √i as a complex number.

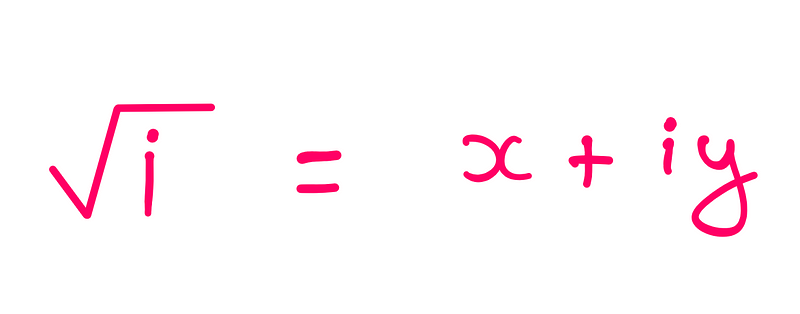
Next, squaring this equation gives us an algebraic system we can solve.

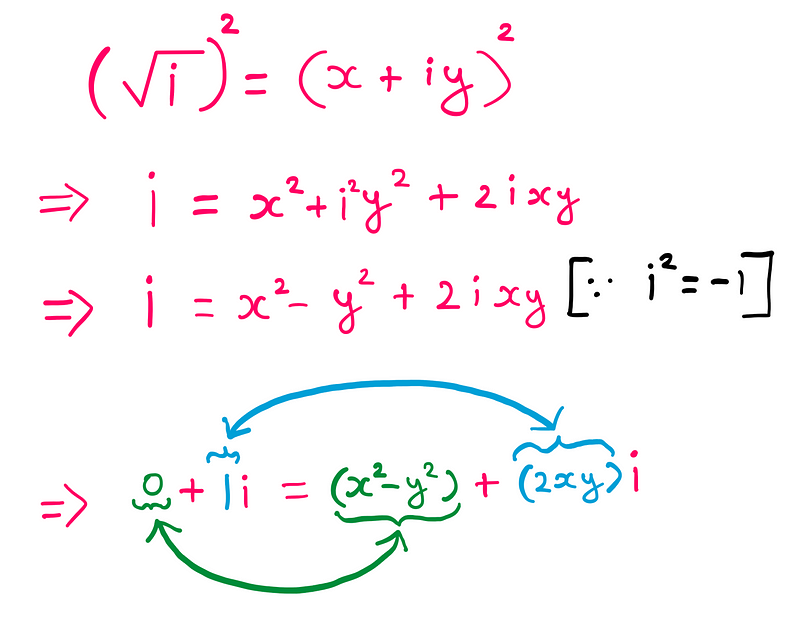
By substituting the values back into the equation for √i, we can arrive at our solution.

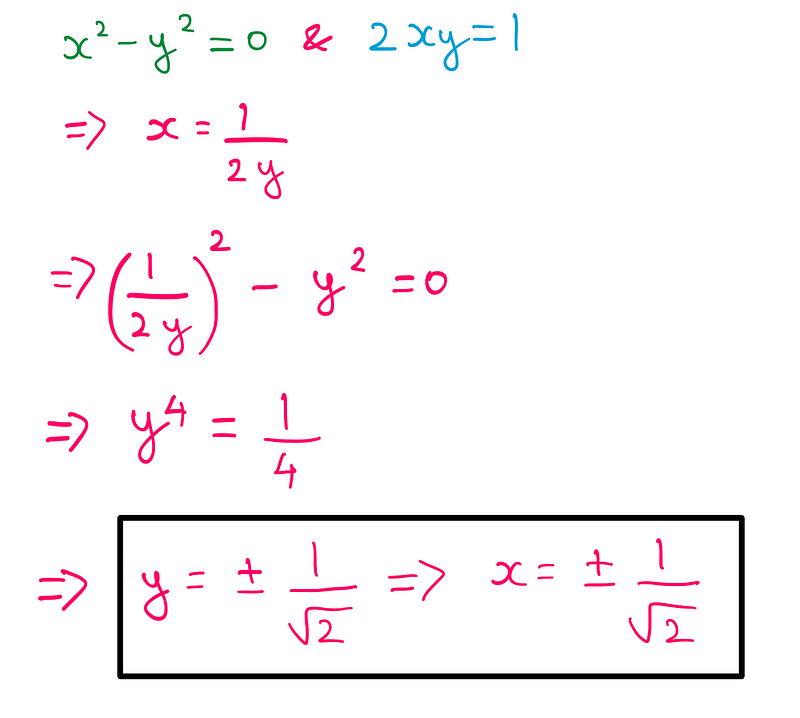
This result answers our initial question, but what does it signify? Let's explore this through a more intuitive lens.

Video Description: In this video, we delve into the concept of calculating the square root of the imaginary unit i, illustrating the process step-by-step.

Section 2.1: Intuitive Understanding of √i

Returning to the complex plane, if we visualize a vector extending from 0 to i, multiplying this vector by i results in a rotation of π/2 radians (or 90°) counterclockwise, leading us to -1. Repeating this multiplication by i rotates the vector again to -i, and further multiplications continue this pattern, cycling through 1 and i.

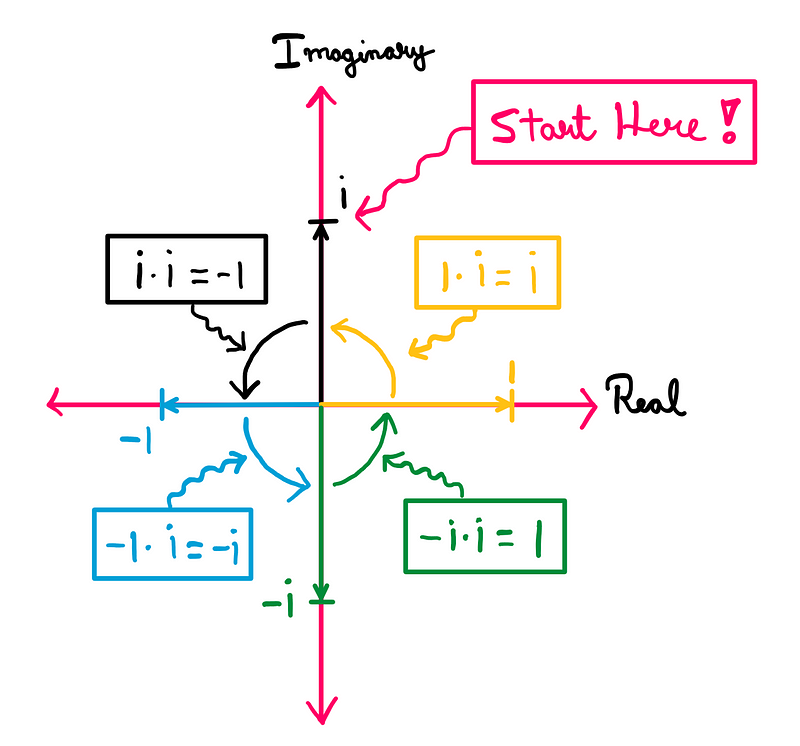
If multiplying by i results in a π/2 radian rotation, then multiplying by √i rotates it by π/4 radians (or 45°). This indicates that √i will have two root points along the unit circle: one at 45° from 1 toward i, and the other at 135° from -1 toward -i.

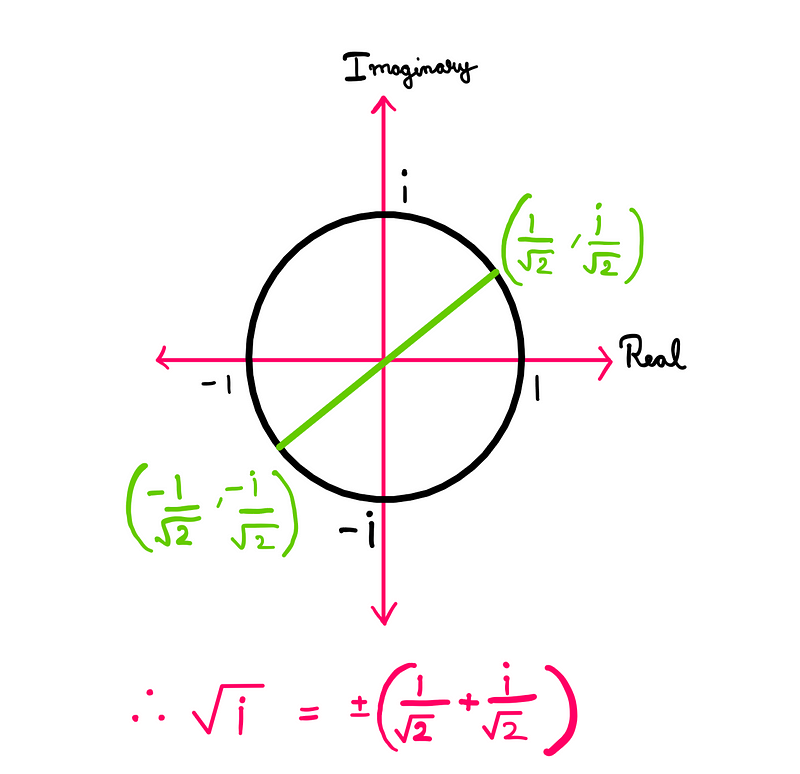
Thus, the seemingly arbitrary x and y values derived from our mathematical approach can be intuitively interpreted as angular divisions of the rotation performed by (1*i) or (-1*-i).

Final Thoughts

In conclusion, we have illustrated how a seemingly 'complex' problem could be resolved with relative ease. The key is to approach challenges with confidence, gradually building a solid foundational understanding.

The principles of complex number theory are integral to various applications, including wave equations and phase calculations, which are essential in modern digital and analog technologies. The problem of calculating √i merely scratches the surface of these applications, offering a glimpse into the intricate framework of contemporary technological devices.

If you found this discussion enlightening and beneficial, I encourage you to show support by clapping, following, or subscribing.

For further reading, consider exploring these topics: How To Intuitively Understand Euler’s Identity? and Logarithms: The Long Forgotten Story Of Scientific Progress.

Video Description: This video provides a comprehensive explanation of √i, showcasing its significance in mathematical theory and practical applications.