Understanding Collisions: Momentum and Kinetic Energy Explained
Written on
Chapter 1: The Basics of Momentum and Kinetic Energy
In the realm of physics, when two objects collide, the principle of momentum conservation comes into play. Momentum (p) is calculated as the product of mass (m) and velocity (v). While kinetic energy also relies on mass and velocity (expressed as 1/2 mv²), it doesn't always follow that kinetic energy is conserved during a collision. Let's delve into this concept.
Simple Collision Between Two Particles
To illustrate, let's consider a basic scenario: a particle with mass m is moving in the x-direction at a velocity v (referred to as particle A) and collides with another stationary particle of mass m (particle B). This is a straightforward head-on collision in a single dimension (the x-direction).
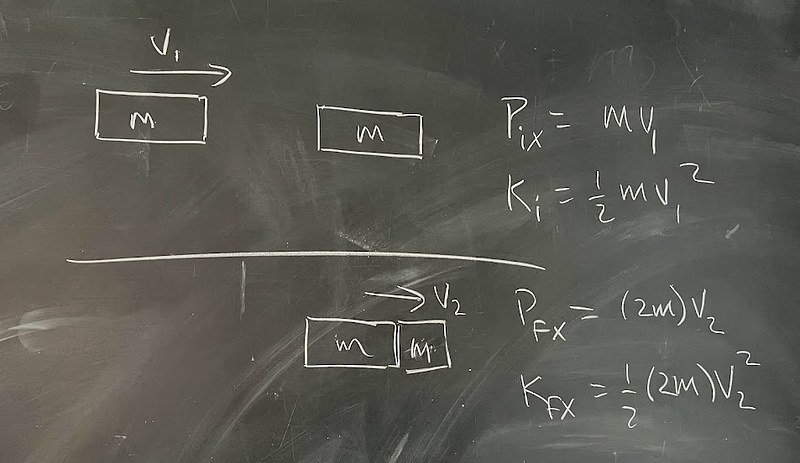
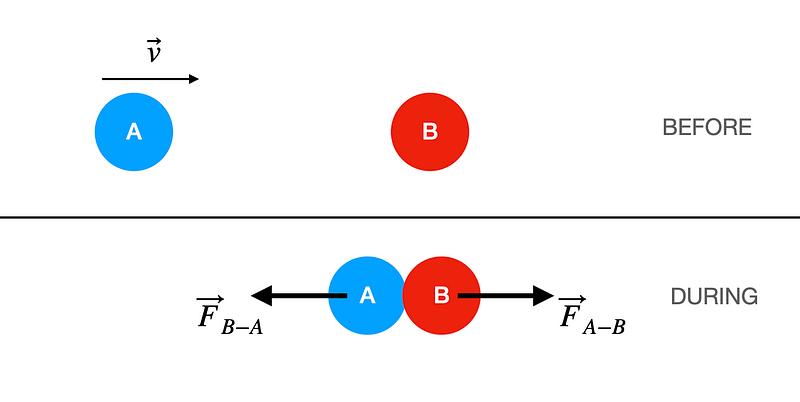
The crucial point is that during the collision, particle A exerts a force on particle B, while particle B simultaneously exerts an equal and opposite force on particle A. This interaction emphasizes Newton's third law of motion.
Momentum Conservation Principle
According to the momentum principle, the change in momentum for particle A must be equal and opposite to that of particle B, assuming the forces act over the same time interval.
This interaction leads to the conservation of momentum, allowing us to derive the final velocities of both particles post-collision. However, simply applying conservation of momentum doesn't yield a unique solution.
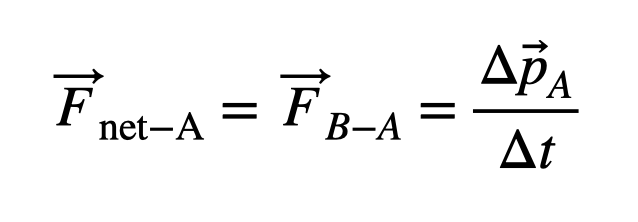
In this case, if we denote the final velocities as v_A for particle A and v_B for particle B, we can express the conservation of momentum equation as follows:
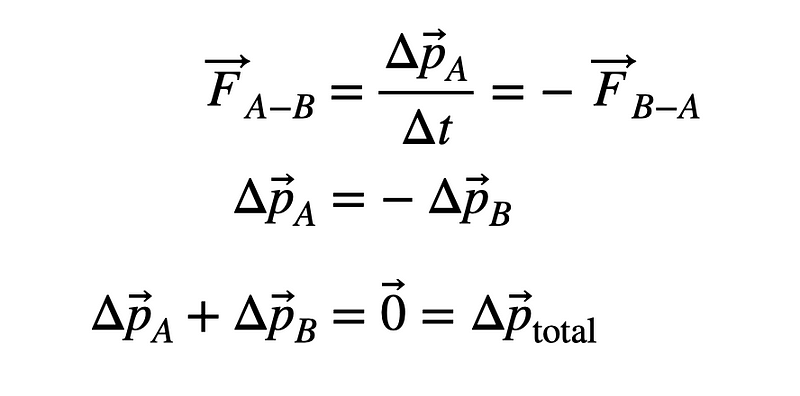
If particle A starts with a velocity of 10 m/s, any combination of v_A and v_B that adds up to 10 m/s will satisfy the momentum conservation equation. However, we cannot solve for the specific final velocities using momentum conservation alone.
Kinetic Energy Conservation in Collisions
Interestingly, in elastic collisions, kinetic energy is also conserved. With both momentum and kinetic energy conservation principles, we can solve for the final velocities of the particles involved.
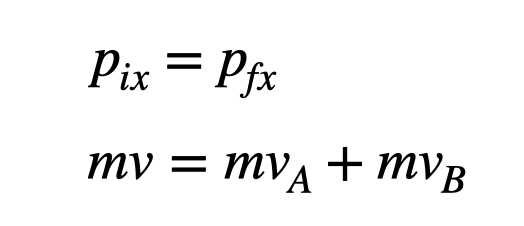
This leads us to conclude that in the specific case of an elastic collision, particle A will come to a halt, while particle B will move forward with the initial velocity of particle A.
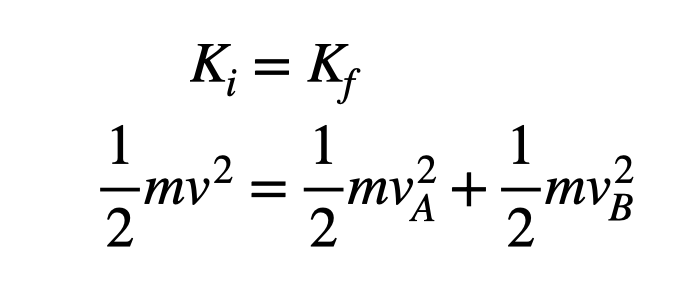
Modeling Elastic Collisions Using Python
To further our understanding, we can model these collisions using Python. The objective is to simulate the movement of the particles, with a spring force acting to separate them if they overlap during a collision.
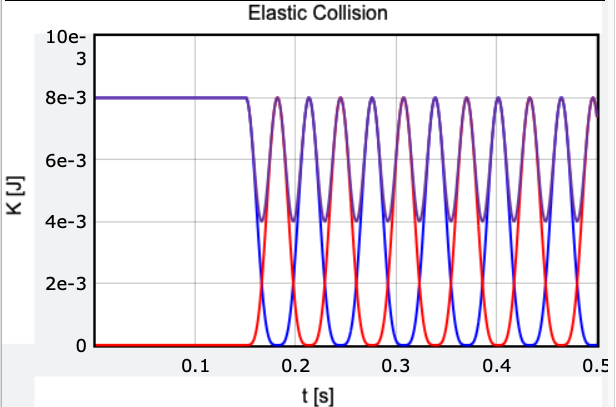
This animation provides a visual representation of elastic collisions.
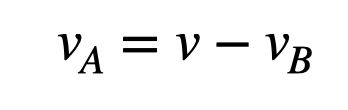
It's fascinating to note that kinetic energy remains conserved in elastic collisions, regardless of the masses or their initial velocities.
Chapter 2: Inelastic Collisions and Energy Transfer
When we examine completely inelastic collisions, where two objects stick together after colliding, we can simplify our momentum conservation equation.
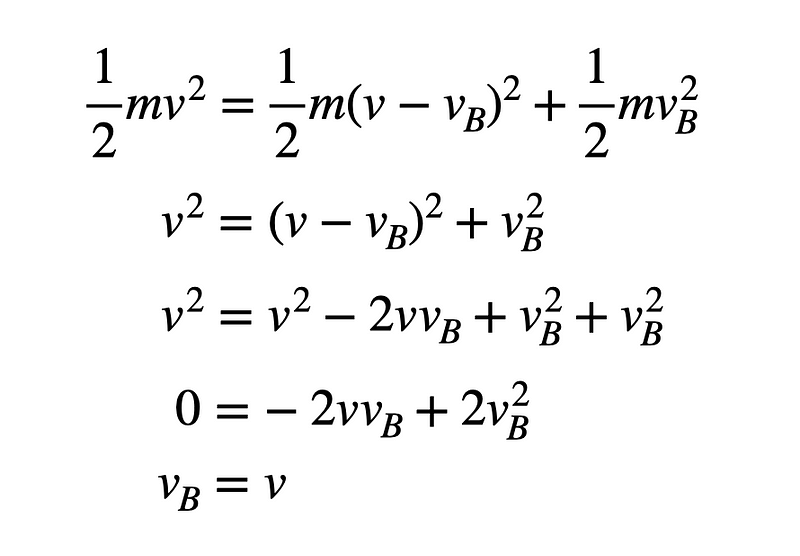
In these scenarios, while momentum is conserved, kinetic energy is not. The final kinetic energy of the combined mass is less than the initial kinetic energy.

This discrepancy raises questions about how momentum can be conserved while kinetic energy is lost, which we can explore through our Python model.

In our simulation, we adjust the model so that the two colliding objects stick together, maintaining the spring force even after collision.
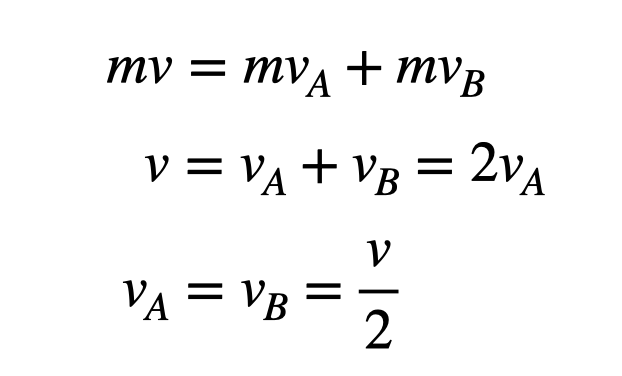
The result showcases that while the two objects appear to move together, their kinetic energy is not constant, leading to a decrease in kinetic energy.
Kinetic Energy Dynamics in Collisions
To visualize the kinetic energy before and after collisions, we can analyze the energy transformations that occur, including potential energy from the spring.
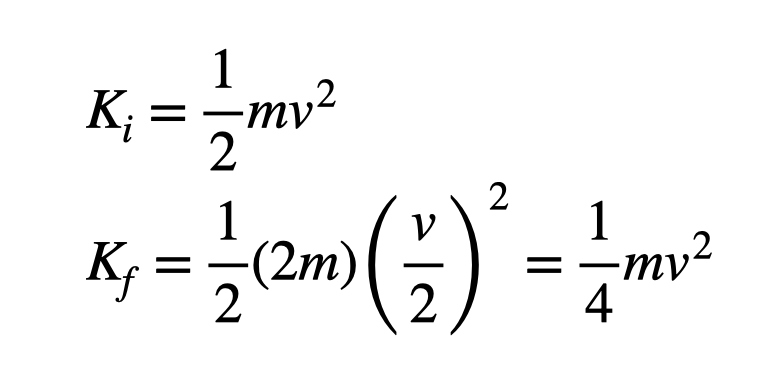
This highlights that kinetic energy is not conserved due to the presence of the spring, which stores energy during the collision.
Exploring Complex Collisions
What happens in collisions that are neither perfectly elastic nor perfectly inelastic? By modeling this in Python, we can explore a scenario where mass B is represented by two masses connected by a spring.

In this setup, momentum remains conserved, while kinetic energy may fluctuate due to internal energy changes within the system.
This dynamic highlights the complexity of real-world collisions, where various forms of energy can influence the outcomes.
A Closer Look at Internal Energy
In any collision, whether elastic or inelastic, the energy may transform into various forms, including thermal, vibrational, or structural energy. These transformations lead to the conclusion that while total energy is conserved, kinetic energy may not be.
This exploration into collisions underscores the intricate balance between different types of energy and the principles of momentum conservation.