Proving the Transcendence of the Euler Number e: A Simplified Approach
Written on
Chapter 1: Understanding Euler's Number
Euler's number, denoted as e, is a key mathematical constant approximately equal to 2.718. This constant can be defined in various ways, one of which is illustrated below:
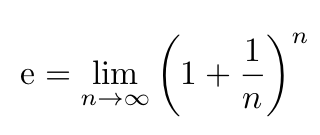
The constant was first identified by the Swiss mathematician Jacob Bernoulli. The primary function associated with e is the exponential function:
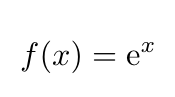
This unique function is significant because it is equal to its own derivative, a property exclusive to exponential functions.
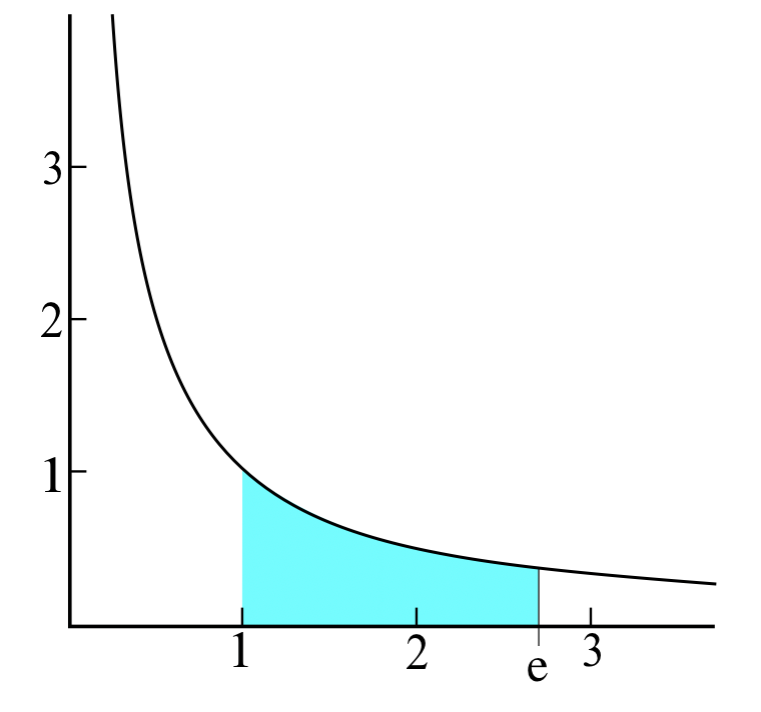
In mathematical analysis, the Euler number e is notably the only number greater than one that renders the shaded area under the curve equal to one.
Transcendental Numbers Explained
Real numbers can be categorized as either algebraic or transcendental. Algebraic numbers can be defined through polynomial equations with integer coefficients, such as:
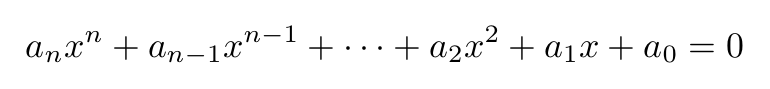
The degree of an algebraic number is determined by the highest power of x that has a non-zero coefficient. On the other hand, transcendental numbers do not satisfy such polynomial equations.
Proving e's Transcendence
The primary objective of this article is to demonstrate that e is indeed a transcendental number. The foundational proof was first established by French mathematician Charles Hermite, but here we present a simplified version attributed to German mathematician David Hilbert.

To begin, we assume the contrary—that e is an algebraic number of some degree n:
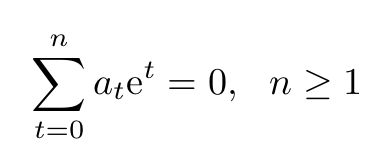
Our proof will analyze the approximation of powers of e with rational numbers. We introduce the following definitions:
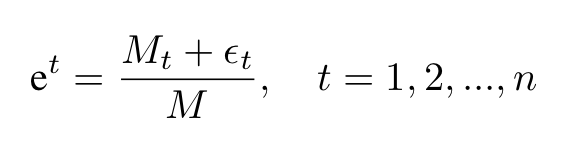
For each power of e in the equation above, we find:
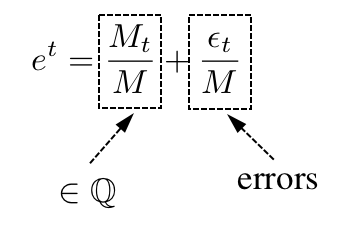
For sufficiently small values of the variable, this implies that all powers of e are remarkably close to rational numbers. Substituting our previous equation into the algebraic equation yields:
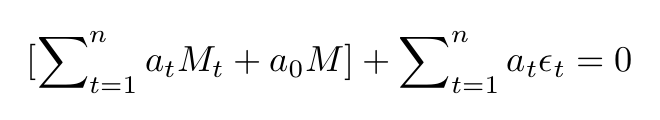
It's crucial to note that the n in both equations is identical. The result from this substitution carries two notable characteristics: the first bracketed expression is an integer, and the M values are chosen to ensure the expression is non-zero. The second expression will be crafted such that its absolute value is less than one.
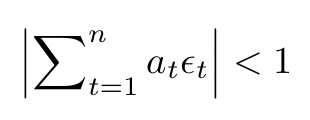
The aim of our proof is to show that this resulting equation cannot hold, creating a contradiction. The sum of a non-zero integer and a quantity with an absolute value less than one cannot equal zero.
Defining Variables for the Proof
Hermite begins by establishing definitions for the M and ε variables. M is defined as follows:
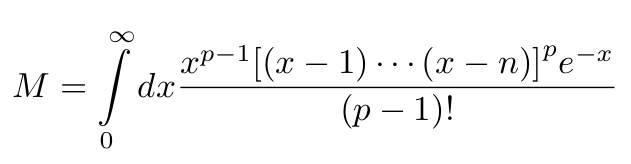
Here, p is a prime number that we will determine later. The choice of p can be made as large as needed while ensuring M remains an integer. The remaining M's and ε's are defined as:
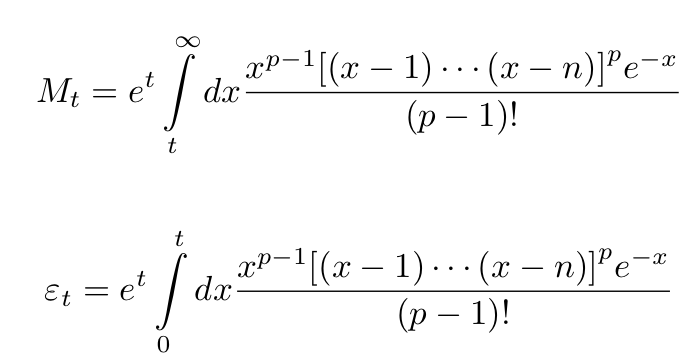
We proceed by selecting p such that the necessary properties are satisfied. Evaluating the integral M involves expanding the binomials in the numerator and raising the result to p:
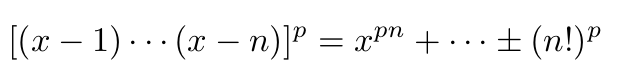
Substituting this into M and applying:
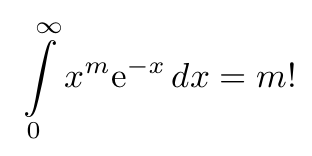
We arrive at:
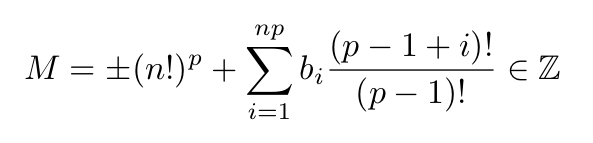
By restricting ourselves to primes larger than n, we can see that the first term is not divisible by p. However, the second term is clearly divisible by p.
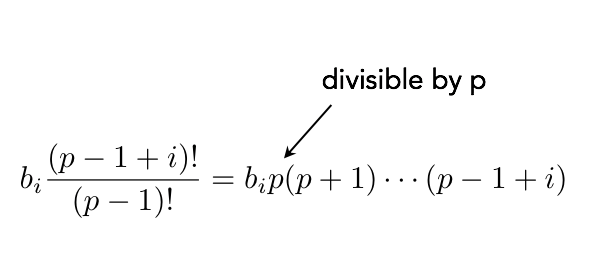
Since M is not divisible by p, the first bracketed term in the equation remains non-zero. We can conclude that this term cannot equal zero as it is not divisible by p.
To establish that the condition holds true, we select a sufficiently large p, leading us to the conclusion:
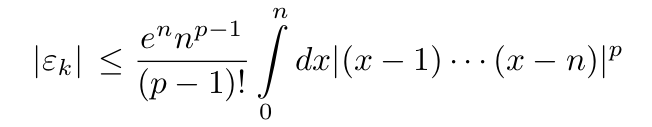
The absolute value of this product has an upper bound, confirming that the proof holds true as p approaches infinity.
This first video, titled "The PROOF: e and pi are transcendental," offers a comprehensive explanation of the concepts surrounding transcendental numbers.
The second video, "e is transcendental -- the best proof!" provides an insightful look into the proof of e's transcendence, complementing our discussion.
For more intriguing content on mathematics and related fields, visit my GitHub and personal website at www.marcotavora.me.