Understanding the Fascinating Properties of Number Manipulation
Written on
Chapter 1: The Mystery of the Number Trick
Have you ever wondered why a peculiar number trick works? When you subtract a number from another, rearranged version of it, the result is consistently divisible by 9. This intriguing observation was shared by Presh Talwalkar on Twitter:

Let’s take a specific example. Consider the integer 74356. If we rearrange the digits to form 46375 and perform the subtraction, we get:
74356 – 46375 = 27981.
Notably, 27981 is divisible by 9, as verified by 27981 / 9 = 3109. This principle holds true for any integer, as demonstrated by Presh Talwalkar. I would like to offer my perspective on this fascinating concept.
Section 1.1: Analyzing the Calculation
Revisiting the previous example, let’s explore the subtraction of 74356 from itself first:

This gives us 0. While 0 is not the answer to our subtraction, it helps us analyze how far off we are from the correct result.
In the first step, we can observe:

In the number 46375, the digit 6 represents 6000. Ideally, we should have subtracted 6000 instead of just 6. Consequently, our adjustment should be 6000 – 6.
Next, let’s examine the second step:

Here, we are subtracting 50. However, since the 5 in 46375 only represents 5, we need to add an extra 50 – 5.
Now, let’s move on to the third step:

In this case, the 3 in 46375 is worth 300, and we are subtracting the correct amount.

However, in step four, we mistakenly subtract 4000 instead of 40000, necessitating an additional subtraction of 40000 – 4000.
Finally, in the last step:

Here, we subtract 70000 instead of 70, which means we need to include an extra 70000 – 70.
Putting it all together, we find:
0 - (6000 – 6) + (50 – 5) - (40000 – 4000) + (70000 – 70) = 27981, which aligns with our original subtraction of 74356 – 46375.
More importantly, observe that all the terms we manipulated can be expressed in the form:
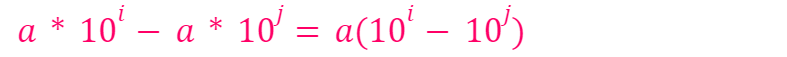
Where a, i, and j are natural numbers with i > j. For instance, 6000 – 6 = 6(1000 – 1). This is particularly relevant since the value of any digit in our decimal system is derived from multiplying that digit by a power of ten.
Section 1.2: The Divisibility Insight
Why does this matter? Because:

Where i and j are natural numbers and i > j, is always divisible by 9! To understand this, let’s consider:
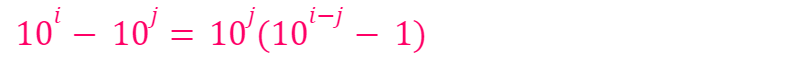
The series 0, 9, 99, 999, etc., all demonstrate divisibility by 9. We can prove this by defining k = i - j, where k > 0.
Then:
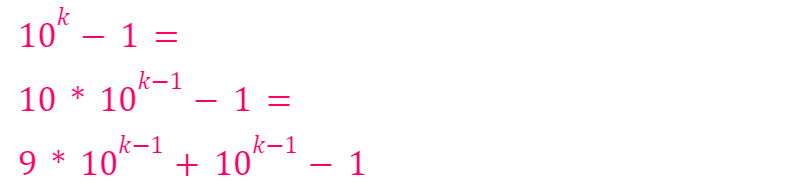
It’s clear that:

is divisible by 9. Furthermore,

This process can be repeated until we arrive at 10? = 1, leading to:
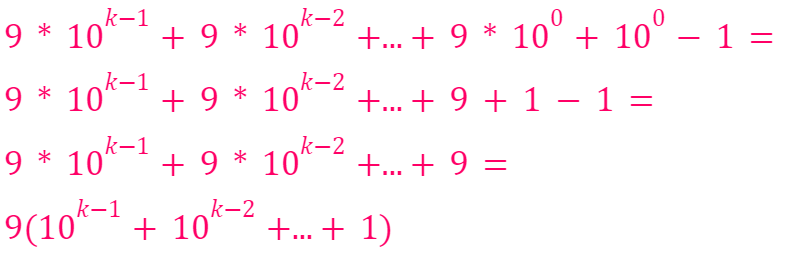
which is evidently divisible by 9 as shown in:
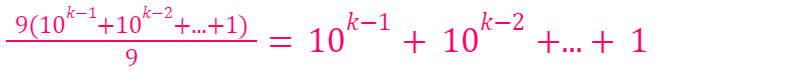
Thus, we’ve established that:

Where i and j are natural numbers and i > j, is divisible by 9. Multiplying this by any integer will yield another number divisible by 9:

Thus:

Where i and j are natural numbers and i > j, must also be divisible by 9. Therefore:

Where i and j are natural numbers and i > j, and consequently:

Where a, i, and j are natural numbers with i > j.
In our calculation of 0 - (6000 – 6) + (50 – 5) - (40000 - 4000) + (70000 - 70) = 27981, all terms are divisible by 9. Since 0 is divisible by 9, any result obtained by adding or subtracting a number divisible by 9 from another number divisible by 9 will also yield a result divisible by 9. This leads us to a fundamental conclusion:

Therefore, the result 27981 must be divisible by 9 due to these properties!
This principle holds universally: regardless of the initial number chosen, subtracting a rearranged version will always yield a result that conforms to this divisibility rule.
Incredible Math Magic Tricks - Explained! - This video showcases various mathematical tricks that will amaze you, revealing the hidden patterns in numbers.
This SIMPLE Maths Trick Will FOOL Everyone!!! - Watch this video to learn a simple yet mind-boggling math trick that can impress anyone!
Thank you for exploring this fascinating topic with us! If you wish to support Street Science, consider contributing on Patreon.