Exploring Time Crystals: Symmetry Breaking in Quantum Mechanics
Written on
Chapter 1: Understanding Time Crystals
In the preceding discussion, we delved into the eigenstates of the Hamiltonian. Our goal was to identify states that exhibit time-translation symmetry breaking. The referenced paper [1] indicates that this quest is akin to discovering Floquet operators with eigenstates that lack 'short-range correlations.' Floquet theory focuses on periodic Hamiltonians and their corresponding eigenstates, suggesting that local operators, when distanced adequately, show no correlation across the examined states.

To explore the ground states of this Hamiltonian that do not adhere to time-translation symmetry, we must first adjust the Hamiltonian to facilitate analysis. By constraining the values within the Hamiltonian, we can simplify our examination and identify straightforward cases that demonstrate time-translation symmetry breaking. Mathematicians and physicists often simplify problems by applying constraints intended to render them more manageable. These constraints are gradually relaxed to observe any resulting changes in behavior; stability in behavior upon perturbation suggests underlying principles at play.
Section 1.1: Simplifying the Hamiltonian
The following argument is derived from paper [1] as we seek a state that disrupts time-translation symmetry. First, arrange particles in a linear formation, assuming that the Hilbert space allows each particle to exhibit either an up-spin or down-spin. If we impose a constraint such that the value along a certain axis is limited to a fixed number, h, we can investigate the implications of decreasing this value.
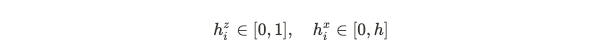
The Hamiltonian that remains focuses solely on the z-components. By setting the x-component to zero, we reduce the Hamiltonian to a simpler form.
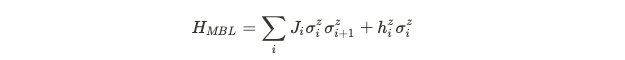
This Hamiltonian yields eigenstates that correspond to specific spin configurations.
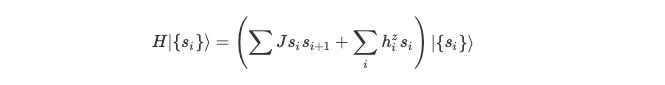
From this Hamiltonian, we can derive a Floquet operator. If we identify entangled eigenstates within the Floquet operator, we achieve our objective. The initial term in the operator is the Hamiltonian itself, influencing time evolution as it is expressed in exponential form. The subsequent term modifies the spins within our eigenstates.
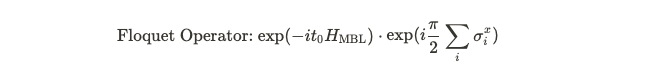
Why does the operator on the left flip spins? The matrices involved are known as Pauli matrices, specifically the x-matrices here, indicated by the superscript x in the summation. These matrices operate on the Hilbert space of a linear arrangement of particles, each in a superposition of up and down spins. For a single particle, we can express the Hilbert space using up and down states as a basis. The Pauli x-matrix is characterized by 1s in its off-diagonal entries, effectively flipping spins:
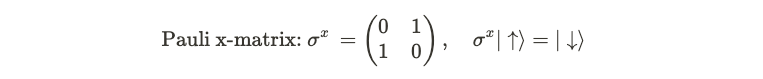
Taking the exponent of the sum of spins can be shown to be equivalent to arranging the operators in a product form.
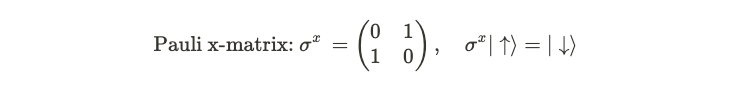
Applying this to the entire one-dimensional line results in the flipping of all spins in the system, as illustrated below:
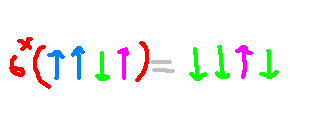
Through the Floquet operator, we can derive a pair of induced eigenstates based on those generated from the Hamiltonian. Verification shows that these eigenstates resemble:
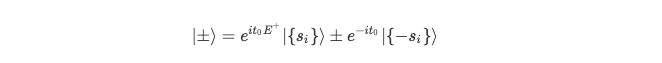
Consequently, we have identified eigenstates that are not short-range correlated, indicating entanglement between spins located in disparate regions. This confirms the existence of states that break time-translation symmetry.
Chapter 2: Video Resources for Further Exploration
The first video, "Matter: You Think You Get It, Then It Turns Into Time Crystals (Part 3 of 3) - YouTube," provides a detailed explanation of the complexities surrounding time crystals, shedding light on their fundamental principles.
The second video, "Time Crystals: Past, Present, and Future - YouTube," discusses the historical context and potential future implications of time crystals, enhancing the understanding of their role in quantum physics.
References
[1] Dominic V. Else, Bela Bauer, and Chetan Nayak. Floquet Time Crystals, arXiv:1603.08001 [cond-mat.dis-nn]