Discover the Radius: A Challenging Geometry Puzzle
Written on
Chapter 1: The Geometry Challenge
In this engaging geometric puzzle, we aim to determine the radius of a circle. This challenge is perfect for anyone familiar with high school geometry and who is willing to think creatively!
To get started, here’s a helpful hint: consider drawing some lines. I encourage you to pause here, take out a pen and paper, and attempt to solve it on your own. Once you feel prepared, continue reading for the solution!
Solution Overview
Let’s denote the radius of the circle as r.
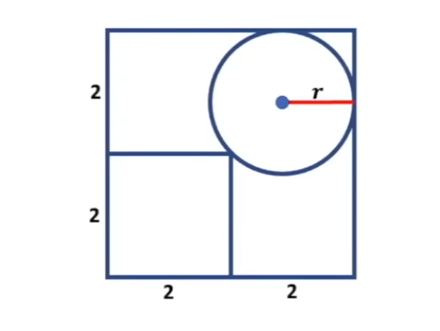
By drawing a diagonal within the smaller 2x2 square, we can gather more information from the provided figure.
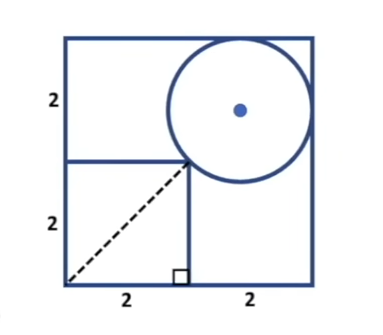
To calculate the diagonal’s length, we apply the Pythagorean Theorem.
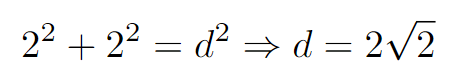
Here, d represents the diagonal. Since we are working with a 4x4 square, the diagonal of the larger square is simply twice that of the diagonal in the smaller square, which equals 4√2.
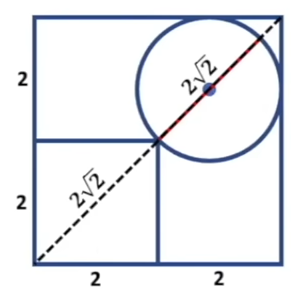
This indicates that the diameter of the circle is slightly less than 2√2. But how can we derive the radius? The trick lies in constructing a smaller square with a side of r in the upper right corner.
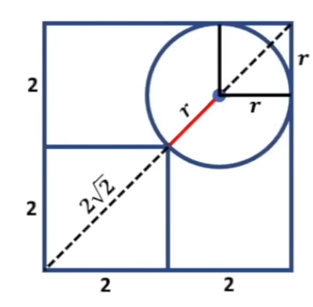
Using the Pythagorean Theorem again, we can find the diagonal length of the r by r square.
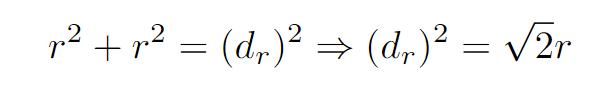
Let’s incorporate this into our diagram.
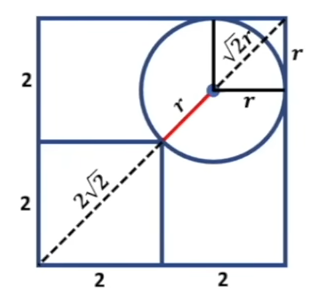
The diagonal of the larger square maintains its length of 4√2. Thus, we can set the two expressions equal to each other.
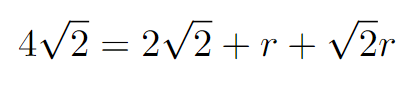
With some algebraic manipulation, we can derive the radius of the circle.
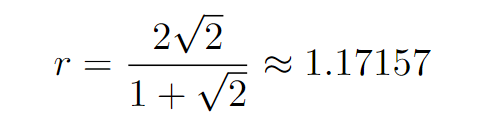
Isn’t that impressive? What were your thoughts while working through this? Feel free to share your insights in the comments below; I’d love to hear from you!
Explore More Math Puzzles
Math enthusiasts, be sure to check out a collection of intriguing puzzles spanning various topics, including Algebra, Geometry, and Calculus. Share these with friends and family for added fun!
The first video, "Only 1% Can Find the Radius of the Given Circle - Geometry Challenge!" presents a fun challenge that tests your ability to find the radius using creative geometric strategies.
In the second video, "How To Solve For The Radius: Challenging 1970s Math Contest!" you'll discover classic techniques for tackling similar problems, enhancing your understanding of geometry.
Thank you for engaging with this puzzle! If you found it enlightening, please show your appreciation by giving it a clap.
